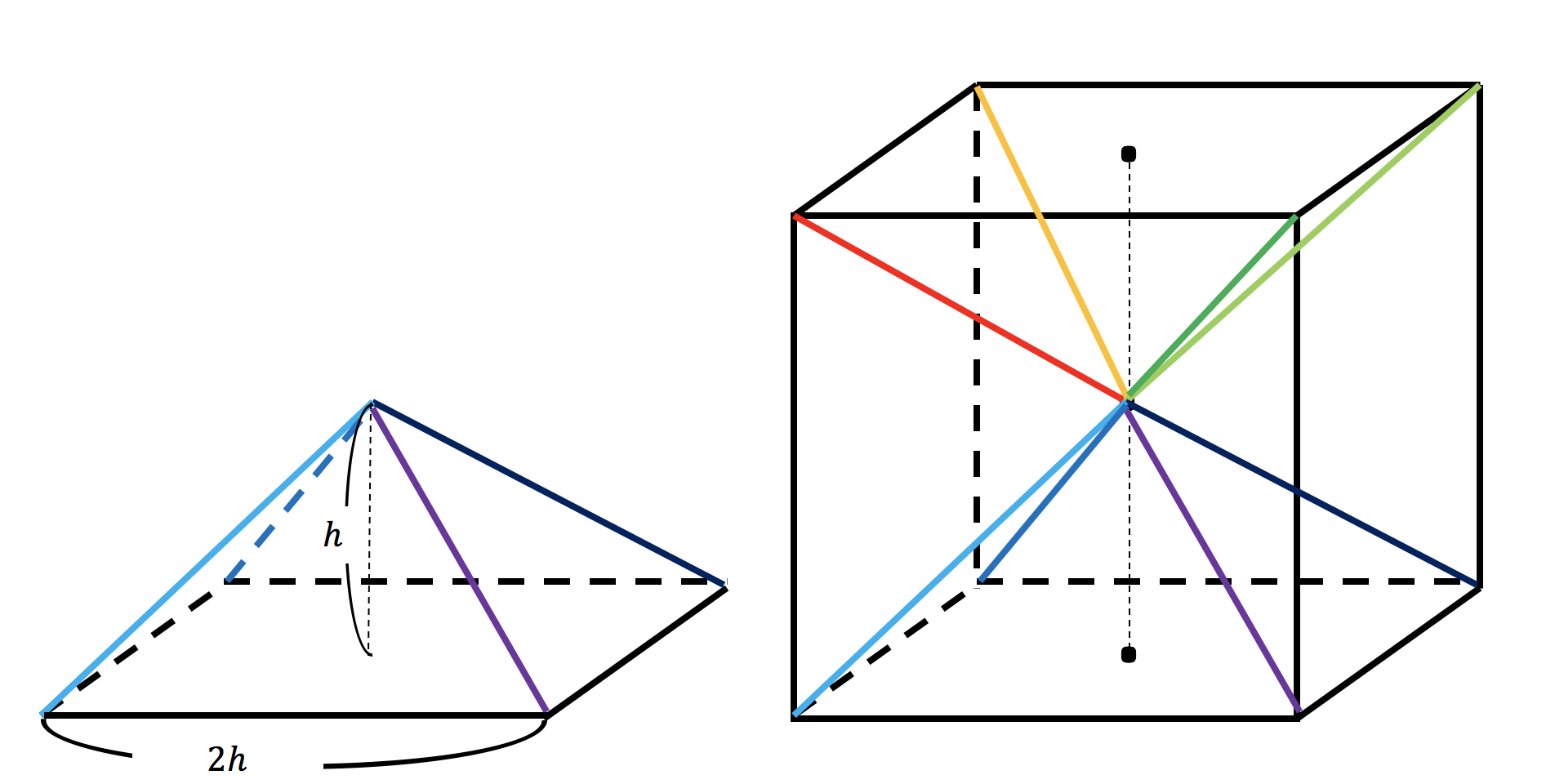
右の図のように,1辺の長さが 4 cmの立方体があり,辺 ab の中点を m ,辺 bc の中点を n とする。この立方体を4点 m, e, g, n を通る平面で2つの立体に切る。 このとき,次の(1)~(5)の各問いに答えなさい。 (4) 2つの立体のうち,頂点 b を含む立体の体積を求めよ。 三角錐の体積の求め方。 下の図は立方体から三角錐を切り取った立体です。 この三角錐の体積が、 1・1・1/2・1・1/3 =1/6 となるそうなのですが、なぜこうなるのか分かりません( ;特殊な四角錐の場合 底面が一辺 2 h 2h 2 h の正方形であるような特殊な正四角錐の場合は,立方体を六個に切ることで簡単に V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h が証明できます。

トップ100 角錐台体積
立方体 三角錐 切断 体積
立方体 三角錐 切断 体積-三角錐の体積の求め方。 下の図は立方体から三角錐を切り取った立体です。 この三角錐の体積が、 1・1・1/2・1・1/3 ≪立方体の体積≫ 12×12×12 =1728 ≪三角すいbfegの体積≫ 1 3 ×{(12×12÷2)×12} =2 ≪立方体-三角すいの体積≫ 1728-2 =1440 ベクトルの問題 右の図のような1辺の長さが4㎝の立方体があります。点iは辺ef上にあり、ei=2㎝です。 この立方体を、3点a,c,iを通る平面で切ります。 このときできる点bを含む立体について、次の問に答えなさい。 (1) この立体の体積は何㎝3ですか。



Eb1 Hcc Edu Tw Edu Data Research Pdf
立方体の中に正四面体 さらにもう \(1\) つ。 もっとも簡単に求める方法です。 ここでは、公式の導出をしてみましょう。 「正四面体は、立方体の内部にある」という、知らないとどうにもならない方法です。 下の図のように、立方体の頂点を結べば、2章 空間図形 48 140 次の図の立体の体積を求めよ。 ⑴ ⑵ 138 次の図の角錐の体積を 求 めよ 。 ⑴ ⑵ ⑶ 141 右の図のよ う に ,1 辺 12 cm の立方体から,3 点 A ,C ,F を通る平 面で切ってできる 2 つの立体のうち,小さい方の立体を取り除いた。だから,体積は, ⑵ 三角錐AMDEと なる。 DAEを底面 とみると高さはMA だから,体積は, 1 2 ×3×4 ×3=18 (cm3) 1 3 × 1 2 ×3×4 ×3=6 (cm3) 171 右の図は1辺が6cmの立方体で,点Mは辺AEの中点である。こ の立方体を次の平面で切るとき,頂点Aをふくむ方の立体の体積を求
三角錐 展開図 中学受験 new movie FdData 中間期末:中学数学 1 年:空間図形 いろいろな立体/正多面体/展開図/空間における平面と直線/回転 3分でなるほど!四角錐の体積・表面積の求め方をマスターしよう! 数スタ 立方体の中にある三角すい たくさんの中学で出題されている問題です。 高さが2cmの二等辺三角形4つを切り取ってできたものです。 これを組み立ててできる四角すいの体積を求めなさい。 ただし、角すいの体積は、 (底面積)× (高さ)÷3で求められます三角錐の体積 当HPの読者のK.S.さんより、平成24年10月10日付けで標記話題をメールで頂いた。 原点をOとし、空間上の3点A(a 1 ,a 2 ,a 3 )、B(b 1 ,b 2 ,b 3 )、C(c 1 ,c 2 ,c 3 )とす
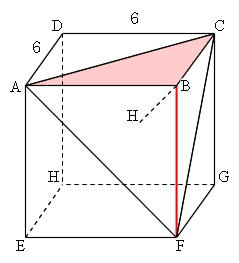
(立方体内に内接する三角錐の重なった部分の体積) 1292 triangular pyramid 長いタイトルだが,その通りで,立体中の三角錐の作る体積を積分で求めようという,別の項で紹介しているが,平成24年郷中ゼミの中で,別講座で実施された内容の授業。) 三角錐の体積は 底面積×高さ×1/3 だそうですか、、 解説お願いします。 (4) 右の図のような, d 1辺の長さが6cmの c a。 立方体 abcd b 36 36 efgh から,三三角錐 cm he bacfを切り取っ た立体の体積を求め なさい。



几何形状平的线象集合抽象图立方体 球形 锥体 棱镜传染媒介例证稀薄的标志为向量例证 插画包括有塑造 几何




數學固體球立方體圓錐棱鏡金字塔立方體圓柱體六邊形金字塔具有體積和曲面公式的幾何圖形向量圖形及更多一個物體圖片 Istock
数学切り抜き帳 正十二面体の中には立方体が隠れている 前回はこのことに着目して正十二面体の体積を求めた.今回はそれと異なる観点と異なる方法で正十二面体の体積を求めてみよう. まず,準備として正五角形の対角線の長さを求める. 正五角形2つの三角錐の体積比を求めなさい。 右の図のような相似である円柱a,bがある。 次の問いに答えなさい。 ①円柱a,bの表面積の比を求めなさい。 ②円柱a,bの体積の比を求めなさい。 相似な2の立方体a,bがあり、相似比は である。 bの体積が ㎤のとき、aの立方体ではどうでしょう。 一辺をaとするとき 二次元正方形の周囲は4a、面積はa² 三次元立方体の表面積は6a²、体積はa³です。 四次元立方体の表面積は8a³、体積はa⁴であることがわかっています。



中1 空間図形 6 立体の体積 2 学習支援 まなびの函



1
④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。 三角柱の体積= 1 2r2 × r よって,1つの 三角錐 の体積は次式で表される. 三角錐 の体積= 1 2r2 × r × 1 3 →「底面積×高さ× 1 3 」になっている.体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!



相似比と体積の計算 円錐台 三角錐台 中学3年数学 Youtube




6种方法来计算三维物体体积
(正五角柱の体積S):(五角錐の体積T)= 5 a : a 3 2 = 5 : 3 2 =15:2 問題 右の図のように,立方体の底面の各辺の中点と,この面と向かい 合う面の対角線の交点を結ぶと正四角錐ができる。このとき,正四 角錐の体積は,立方体の体積の何倍になるかを下の図によって三角錐の体積の求め方を考えます。 上の図のように縦横高さが等しい立方体を半分に切った三角柱を考えると、 この三角柱は、上図のように、体積が等しい(底面積が等しく高さが元の立方体の辺の長さの)3つの三角錐に切り分けることができます。 それで、三角錐のよって立方体の体積をWとすると W = 2h ×2h ×2h = 8h3 W = 2 h × 2 h × 2 h = 8 h 3



呆哥数学立体几何 简单几何体的表面积与体积 6 知乎




三角体体积的计算公式 搜狗图片搜索
立方体と分割合同な三角錐の構成について(小森・利根川・雪田) 1 立方体と分割合同な三角錐の構成について 小森 洋平・利根川真隆・雪田 友成 早稲田大学 教育・総合科学学術院 学術研究(自然科学編)第65 号 1 ~14 ページ,17 年3 月三角錐でも良いが、すべての面が合同な正三角形なので正四面体が最も適切である。 (2) 正四面体acfhの体積を直接出すことは無理なので、 立方体から、いらない部分を引き算して求める。 いらない部分は全て同じ形の三角錐である。してみると,ao は三角錐aoefにおける高さとなる。 また,∠eof =90゜,oe=ofより, oef は直角二 等辺三角形になることがわかるので, 三角錐aoef =3×3× 1 2 ×6× 1 3 =9 cm3 となります。 三角錐oaef=三角錐aoef より,求める体積は9cm3 (3)体積を表す式から高




4d F736f F D3344b773b5f8acc92d2daac5b6a1b458a6f3aabab0caba41a765b27b2dbcc6bec7a470bdd7a4e52e646f63 Pdf 免费下载




四面體 維基百科 自由的百科全書
立方体の体積 下図が立方体です。立方体は全ての辺が同じ長さなので、体積の計算も簡単です。縦×横×高さを計算すれば良いですね。 よって、 立方体の体積=4×4×4=64cm 3 です。 立方体の体積は?1分でわかる計算、単位、公式、求め方、リットルとの関係立方体の体積比になる。 例4)慣性モーメントの計算 例3で計算した三角錐のz軸の周りについての慣性モーメントの計算を行う。 まず、解析的に計算を試みる。 プログラムでは以下のように書くことが 2次元の正3角形、3次元の正4面体を延長した、4次元空間にある正三角錐の体積はいくつになるか。 さらに延長して、一般にN次元の正三角錐の体積はいくつになるか。 4次元空間にある正三角錐のような図形は、正五胞体というのだそうだ >> wikipedia正五胞体。 ウィキペディアには『超体積




正四面体 Wikiwand



立方体内に内接する三角錐の重なった部分の体積 Triangular Pyramid
それは、 (三角錐の体積)= (底面積)× (高さ)× です。 三角柱であれば、 (三角錐の体積)= (底面積)× (高さ) で求めることができます。



1




なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 4 4



立体三角形体积公式 搜狗搜索




三角圆锥体 新人首单立减十元 21年8月 淘宝海外




圆面积与球体积的统一探讨 参考网




直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




6种方法来计算三维物体体积




七胞體 Wikiwand



直角三角体体积公式三角形体积计算公式 直角三角锥体怎么算体积 好基网络




錐體體積公式
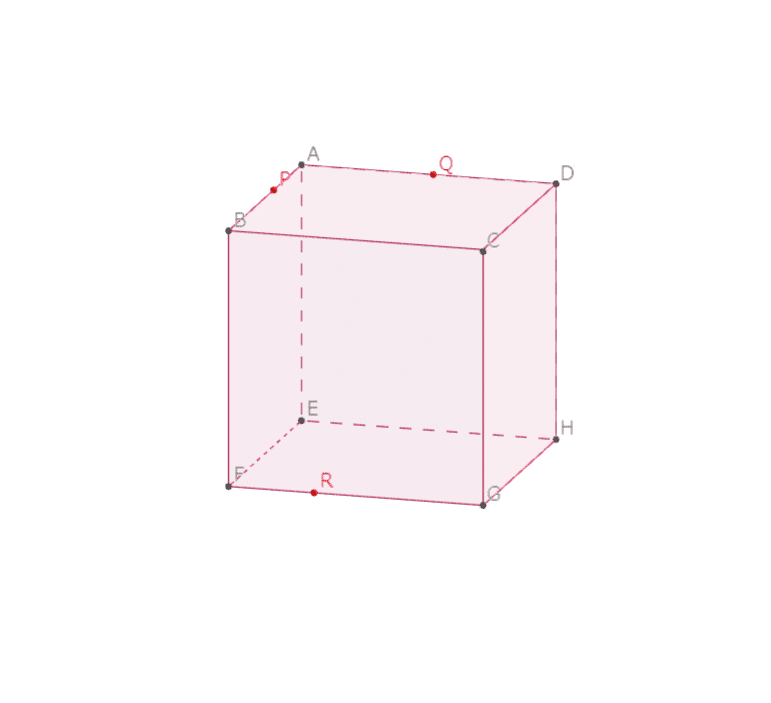



立方体の切断 切断箇所の位置や立体の体積を求める場合 直角三角形や三角錐の相似に注目する 立方体 の切断で切り口が正六角形になるとき 切断されてできた立体は同じ形になる ワンセンテンス算数 Note




截头圆锥体体积 表面积 质量计算公式与在线计算器 三贝计算网 23bei Com
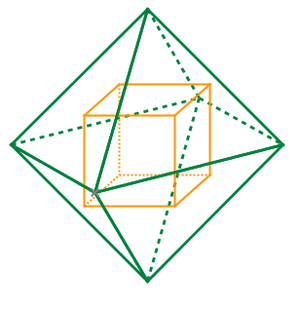



立方體 Wikiwand




算数 113 立方体から三角すいを3つ切り取る 附設 立体図形 Youtube



直角三角体体积公式三角形体积计算公式 直角三角锥体怎么算体积 好基网络



三角锥体积计算公式 三角锥形体积公式 三角柱体积计算公式




112cm Abcd Efgh D C Descubre Como Resolverlo En Qanda




切り取った三角錐と 元の立方体の体積の比を教えてください Clear




6种方法来计算三维物体体积




立方體 Wikiwand




討論 請問正四面體的畫法



一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋




錐體英文




锥形长方体体积形状光学错觉 找到长方体的体积png图片素材免费下载 图片编号 Png素材网



Math 錐体の一部の体積 働きアリ The 2nd
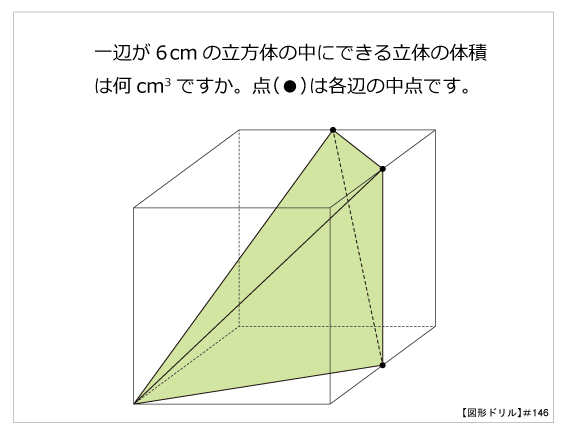



図形ドリル 第146問 立体の体積 算数星人のweb問題集 中学受験算数の問題に挑戦




トップ100 角錐台体積



五彩的立方体素材下载 欧莱凯设计网 08php Com




体積の求め方 計算公式一覧




六面體 Owlapps



求体积 锥体及高维锥体体积公式推导 哔哩哔哩 つロ干杯 Bilibili




正立方體與正三角錐 1 Youtube




角錐體積公式的由來 Youtube



Eb1 Hcc Edu Tw Edu Data Research Pdf




体積の求め方 計算公式一覧
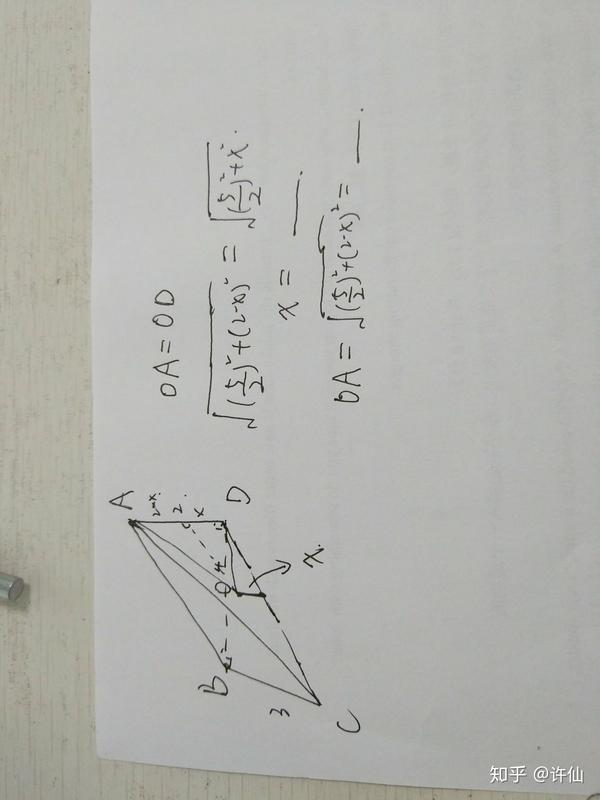



高中数学中三角锥 立方体等的各种外接球内接球半径求法 三角锥内接球半径公式 爱在网




立方體 Wikiwand




研發養成所 Bridan S Blog 4rdp For R D Person 立方體六分之一的提示 1 6 Cube
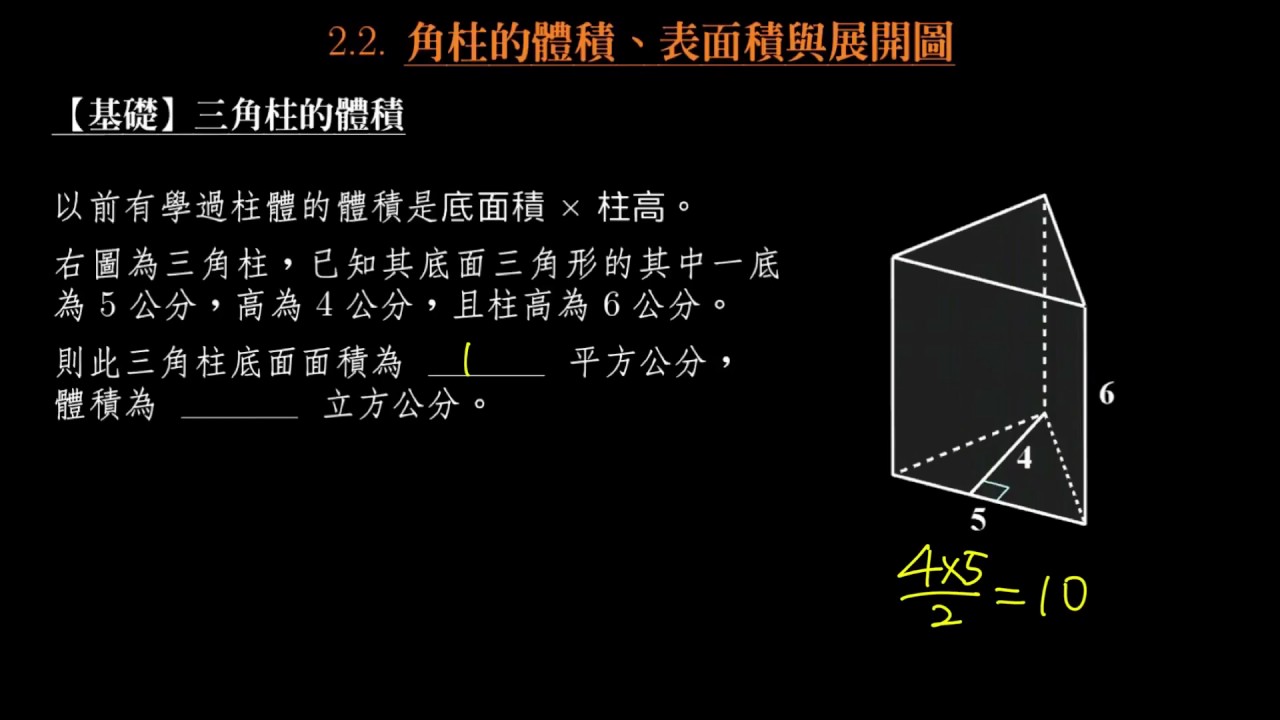



基礎 三角柱的體積 Youtube



三角锥形面积公式三角形的体积公式是什么 银颜网




三角立方体体积公式 三角体体积计算公式 三人行教育网 Www 3rxing Org



正四面體 維基百科 自由的百科全書
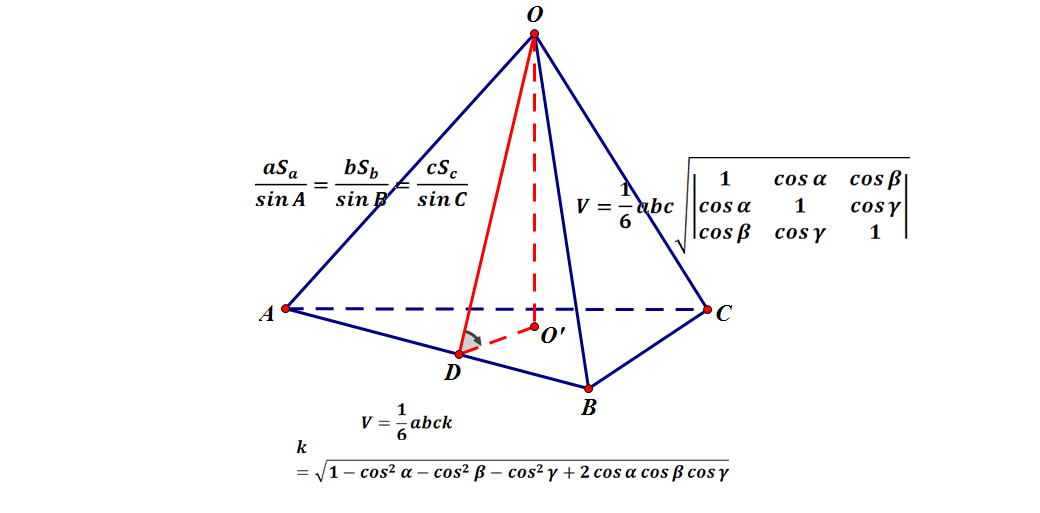



四面体体积公式 知乎




四面体体积理论三角形立方体 5png图片素材免费下载 图片编号 Png素材网




梯形体体积计算公式与在线计算器 三贝计算网 23bei Com




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




复合八面体立方体 Wikiwand




掌握這些知識點再也不怕立體截面圖形題了 每日頭條



体积几何形状 球体 锥体 圆柱体 立方体 金字塔 视角要素 一组矢量插图 学校的数学数字 库存矢量图 免版税




四角柱 维基百科 自由的百科全书



数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋




圆锥体体积 表面积 质量在线计算器 三贝计算网 23bei Com



数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋



圆锥的体积计算公式 万图壁纸网



锥体的体积公式中1 3是怎么来的 知乎



Math 空間図形 立体の切断と切り口 働きアリ The 2nd



こういうタイプのって 赤い三角形と頂点1つで作られた三角 Yahoo 知恵袋



立方体の中にある三角すい 算数解法の極意



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ



1




四面體 維基百科 自由的百科全書



漫谈超球体的体积公式 知乎




六年級 奧數知識點 立體圖形的計算 每日頭條



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



1立方米等于多少立方厘米



1



三角形立方怎么算 图片欣赏中心 急不急图文 Jpjww Com



1辺6センチの立方体abcdefghから立体abcfを切り取った立体の体 Yahoo 知恵袋




1辺aの正四面体の体積 身勝手な主張




棱锥 维基百科 自由的百科全书




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




立方体の切断 切断箇所の位置や立体の体積を求める場合 直角三角形や三角錐の相似に注目する 立方体 の切断で切り口が正六角形になるとき 切断されてできた立体は同じ形になる ワンセンテンス算数 Note




最も欲しかった 正四面体三角錐




如何求立方体 棱柱体和棱锥体的体积 Find The Volume Of Cube Prism And Pyramid Tl80互动问答网



学習支援 まなびの函 中1 空間図形 6 立体の体積 2



立方体から三角錐を切り取る Cut Out A Triangular Pyramid From Cubes Youtube




1辺aの正四面体の体積 身勝手な主張



三角锥形面积公式三角形的体积公式是什么 银颜网




怎么计算圆锥体的体积 最有妙招网



Http Www Goodschool Com Tw Doc Www Goodschool Com Tw Concept Pdf




トップ100 角錐台体積



三角体积木图片 万图壁纸网



Http Www Goodschool Com Tw Doc Www Goodschool Com Tw Concept Pdf



三角体积木图片 万图壁纸网



Mathematics 三平方の定理 5 空間図形と三平方の定理 働きアリ



立体図形の切り口 第13問 巣鴨中学 06年 立教新座中学 08年 算数受験問題 類題 まいにち一題 中学受験過去問題研究




长方体表面积体积立方体png图片素材免费下载 图片编号 Png素材网




时尚彩虹渐变立方体三角形素材下载 欧莱凯设计网 08php Com




この 中にある三角錐の体積の求め方が分かりません 解説お願いします Clear



五彩三角锥形素材下载 欧莱凯设计网 08php Com



三角锥数字步骤素材下载 欧莱凯设计网 08php Com



0 件のコメント:
コメントを投稿