一次方程式の解き方 (かっこ、小数、分数) PR この広告は3ヶ月以上更新がないため表示されています。 ホームページを更新後24時間以内に表示されなくなります。 左辺から8を引くのであれば、右辺からも8を引かなければなりません。 2X+8−8=−12−8 −2X=− するとルールで学んだことを使います。 左辺の2が邪魔なので、両辺を2で割ってあげればいいんですね。 すると x=10 よって、解は10ということになります。 じゃあ、移項ってこんなに面倒なのかというと、これは本来の仕組みを説明しただけで、実際は この記事では、一次方程式の解き方について解説していきます。 一次方程式の解く手順は? かっこ、分数、小数があるときの解き方は? などなど、一次方程式のあらゆるパターンの解き方について例題を通して説明していきます。
2 27第2章いろいろな連立方程式 分数を含む連立方程式 プログラミングの雫
方程式解き方 分数
方程式解き方 分数-方程式と分数の関係 下記の分数を含む方程式を解きましょう。 分数はできる限り整数に変換します。1問目は、 です。2問目は分母にxがあります。ポイントは「1/x=」の状態にして、両辺の逆数をとります。 まとめ 今回は方程式について説明しました。意味が理解頂けたと思います。方程式は、ある特定の数のとき成立する等式です。等号、未知数、恒等式など関係 方程式の問題の解き方(2):逆数をかける (例)方程式 2 x = 6 を解いてください これも方程式を解いてください、じゃから、「x = 」の形を目指すわけじゃな 数学おじさん そのためには、 まず、問題の式と、目的の式をよーく見比べてみてほしいん




連立方程式 分数を含む計算の解き方をイチから解説 Youtube
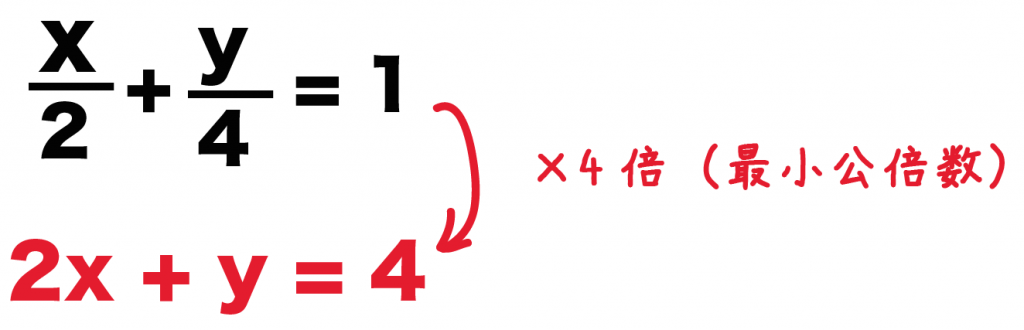
じゃあどうやって二次方程式から分数を削除するのかっていうと、 分母の最小公倍数を両辺にかければいいんだ。 この分数の消し方は、 分数を含む一次方程式の解き方;今回の記事では、 分数、小数、ルート、置き換え、絶対値を含む二次方程式 など ちょっと複雑な二次方程式の解き方についてまとめていきます。 二次方程式の基礎問題についてはこちら! > 二次方程式問題の解説付き! 解き方をパターン別に説明していくよ! Contents 小数を含む二次方程式 分数を含む二次方程式 正直、連立方程式の文章題なんてクソクラエと思ってたよ笑 今日は、そんな中学生のために、 連立方程式の文章題の解き方 をわかりやすく解説してみたよ。 よかったら参考にしてみてね^^ 連立方程式の文章題の解き方がわかる3ステップ 例題をとき
分数と整数が含まれる計算のやり方 かず先生 分母にある数の 最小公倍数をかけて分母を消すべし! 分数を含む方程式は、そのままだと計算が難しいです。 そのため、まずは分母にある数の最小公倍数を両辺にかけて分数を無くしましょう。 例えば、このような方程式であれば分母にある数の最小公倍数12を両辺にかけましょう。 すると、このように かずのかず 「方程式とその解」については 中1数学「方程式とその解」の問題 どこよりも簡単な解き方・求め方 数学では分からない数量を文字(等)で置いて等式を作り、その等式を使って数量を求めることができます この「まだ分かっていないのような分数不等式は両辺に{f(x)g(x)}2を掛けて f(x)g(x)s(x)t(x)>0と変形して解くことができます. ただし,≧0の場合は f(x)g(x)s(x)t(x)≧0かつf(x)≠0, g(x)≠0です. (元の分数不等式において,分子が0になるのはよいが,分母が0になってはいけないから.) Bの方法のまとめ >0 ←→f(x)g(x)s(x)t(x)>0
一次方程式はイコールのバランスさえ取れていれば、両辺にをかけたって、100をかけたっていいわけですから。 一次方程式の分数の問題の解き方。 それは「分母じゃま!」と考えることから始めればよいと思います。 スポンサーリンク分数の式が苦手っていう人は多いと思う。でも、方程式で分数を消すのは、難しくないよ。 まず左側を見ると、 分母が3だね。だから、これには3をかけて、分数を消したい ね。 右側を見ると、 分母が7だね。これには7をかけて、分数を消したい ね。・ 連立方程式を進んで解こうとする。 ・ 連立方程式を解くには、既習である文字1つの方程式を導けばよいことに気付くことがで きる。 ・ 加減法による連立方程式の解き方(2つの式をたしたりひいたりして解く)を理解する。



分数をふくむ1次方程式計算問題




一次方程式 移項を使う問題の解き方と文章題のコツ リョースケ大学
東京都品川区・武蔵小山の《学習塾 Dear Hope》です。 大学受験に向けた数学のテクニックを紹介しています。 難関大を目指す皆さんにぜひ知って方程式の必要性や意味、また方程式の中の文字や解の意味を理解し、等式の性質を使って方程式を解く練習、簡単な1次方程式を解く練習ができるプリントです。 方程式の解き方 (1) 答え 方程式の解き方 (2) 答え 方程式の解き方 (3) 答え 方程式方程式 「8 x =5 x -21」 を解いてみよう。 数学的活動 〔観察、操作などの具体的な活動〕 右辺の5 x をどうすれば、方程式を解くことができるか考える。 解の意味を確認することで、方程式の解き方を考える。 5 x を右辺から左辺に移項することを




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト
分数や小数のある方程式は、両辺に適当な数を かけて、分数 一次方程式の解き方 ① 係数に分数や少数を含むときは、係 数が整数になるように直す。かっこ があればはずす。 ② 文字の項を左辺に、数の項を右辺に 移項してまとめる。 ③ 計算して、「ax=b」の形にする。 ④ 両辺をxの3x5 4 2x= 2x7 6 3 4 両辺に12をかけて分母をはらう 3 (3x5)24x=2 (2x7)9 分配法則でカッコをひらく 9x1524x=4x149 移項して同類項をまとめる 9x24x4x= 19x=38 両辺を19で割る x=2 7x8 9 = 10x 6 2x 4 3 両辺に18をかけて分母をはらう 2 (7x8)=3 (10x)36x24 分配法則でカッコをひらく 14x16=303x36x24 移項して同類項をまとめる 二次方程式は「①解の公式②因数分解③√」による解き方で解きます。 本記事では「二次方程式とは何か」という説明から、3つの解き方の使い分けまでを解説します。 もし、上の3つの二次方程式の解き方を使 55 akk 部分分数分解の公式とやり方を解説! あなたは部分分数



中1 一次方程式の分数は整数になおそう 中学数学の方程式 中間 期末テスト 高校入試対策




1次方程式の解き方 その3 算数 数学が好きになりmath
変数分離形の微分方程式の解き方 変数分離形の微分方程式は、\((2)\) の関係式で解くことができます。 つまり、 \ g(y) \frac{dy}{dx} = f(x) \ という形の式は、次のように \(f(x)\) と \(g(y)\) を積分することで、微分方程式を解くことができます。 \ \int g(y) dy = \int f(x) dx C \ これは、形式的にはX の方程式は, x= (数字) の形になったら「解けた」と言います。つまり, x の係数を 1 にすれば解けます。 1x= (数字) 次の例は,分数の形をしている方程式を解く手順を示しています。方を復習しました。この節ではそれを前提に連立の2次方程式の解き方を紹介し ます。 連立2次方程式の一般論はかなりの準備が必要となるのでここでは扱わず,後 で必要となる特別な形の方程式の解き方だけを身につけてもらうことを目標とし ています。




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




中学2年数学 分数と小数の連立方程式 勉強 Youtube スタディチューブ
分数方程式 ぶんすうほうていしき fractional equation たとえば のように,未知数についての分数式を含む方程式を分数方程式という。 分数方程式を解くには,分母をはらって得られる方程式を解けばよいが,そうして得られた値が,必ずしももとの分数方程式の根となるとはかぎらない。方程式を、 2 x 4=10 から x =3 のように x = の形に変換することを、 方程式を解く と言います。ここでは一次方程式の解き方を解説していきます。 方程式の基本 方程式を解くに当たって基本となるのは、 移行・同類項の計算・左辺を文字のみにする の3つ分数を含む方程式は係数がすべて整数になるように変形して( 分母をはらって )式を簡単にします。 例題②次の連立方程式を解きなさい。 \begin{eqnarray} \begin{cases} 3x 2y = 6 ・・・① & \\ \frac{1}{4}x \frac{2}{3}y = 1 ・・・② & \end{cases} \end{eqnarray}




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者
一次方程式 1次方程式(小数分数11) 無料で使える中学学習プリント http//chugakumanabihirobanet/ 1 1次方程式の解き方(小数「分数形の不定方程式の解き方」 についてイチから解説していきます。 分数形の不定方程式には、 文字が2種類のとき、3種類のときの2パターンがあります。 どちらも質問が多い問題なので、解き方と考え方をこちらの記事でまとめておきますね! 高次方程式の解き方は3つあるので、どの解き方を使うかが重要です。最後には、計算問題も用意した充実の内容です。ぜひこれで高次方程式をマスターしましょう! 数列の基本3|1乗和,2乗和,3乗和の公式と導出 数列の基本4|階差数列の一般項と公式 数列の基本5|部分分数




高校数学 様々な2次方程式の解法 分数 小数 根号 置換 絶対値 受験の月




分数の連立方程式 Youtube
1字方程式の解き方 (1)少数・分数をふくむときは両辺に同じ数をかけて,係数を整数にします。 また,かっこがあったらかっこをはずします。 (2)xの項はすべて左辺に,数の項は右辺に移項します。 移項すると符号が変わります。ルートや分数の指数計算が苦手なひとも多いですよね。 問題② 次の方程式を解いてみよう。 (1) \displaystyle 8^ {x}=\frac {1} {16} (2) 2^ {1x}=\sqrt 3 {2} (1)は両辺を底2の累乗に直しましょう。 \begin {eqnarray} \displaystyle 8^ {x}&=&\frac {1} {16}\\ \displaystyle 2^ {3x}&=&\frac {1} {2^ {4}}\\ 2^ {3x}&=&2^ {4}\\ 3x&=&4\\ \displaystyle x&=&\frac {4} {3} \end {eqnarray}




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




二次方程式とは 見分け方が簡単にわかる中学レベルの問題 中学や高校の数学の計算問題



2




中3数学 分数を含む二次方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




連立方程式の問題 高校の範囲でも登場する大切な分野だ 中学や高校の数学の計算問題
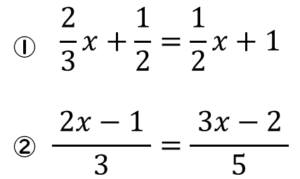



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす
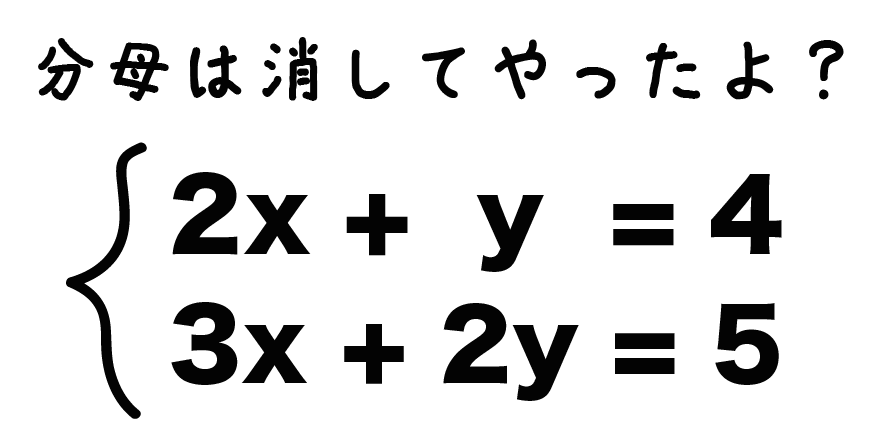



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく



一次方程式の分数の解き方 やさしく解説
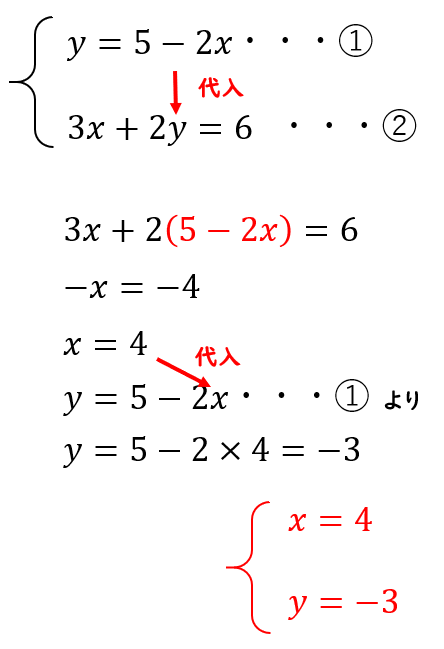



連立方程式の2つの解き方 代入法 加減法 数学fun




分数が含まれている連立方程式の解き方 全国 中学数学ができるようになるブログ




1次方程式の解き方 1 無料で使える中学学習プリント



2 27第2章いろいろな連立方程式 分数を含む連立方程式 プログラミングの雫




โน ตของ 一次方程式 中1 練習問題あり答えあり ช น Junior Clear




連立方程式 いろいろな計算 無料で使える中学学習プリント




例題付き 連立方程式の解き方と失敗しないコツ
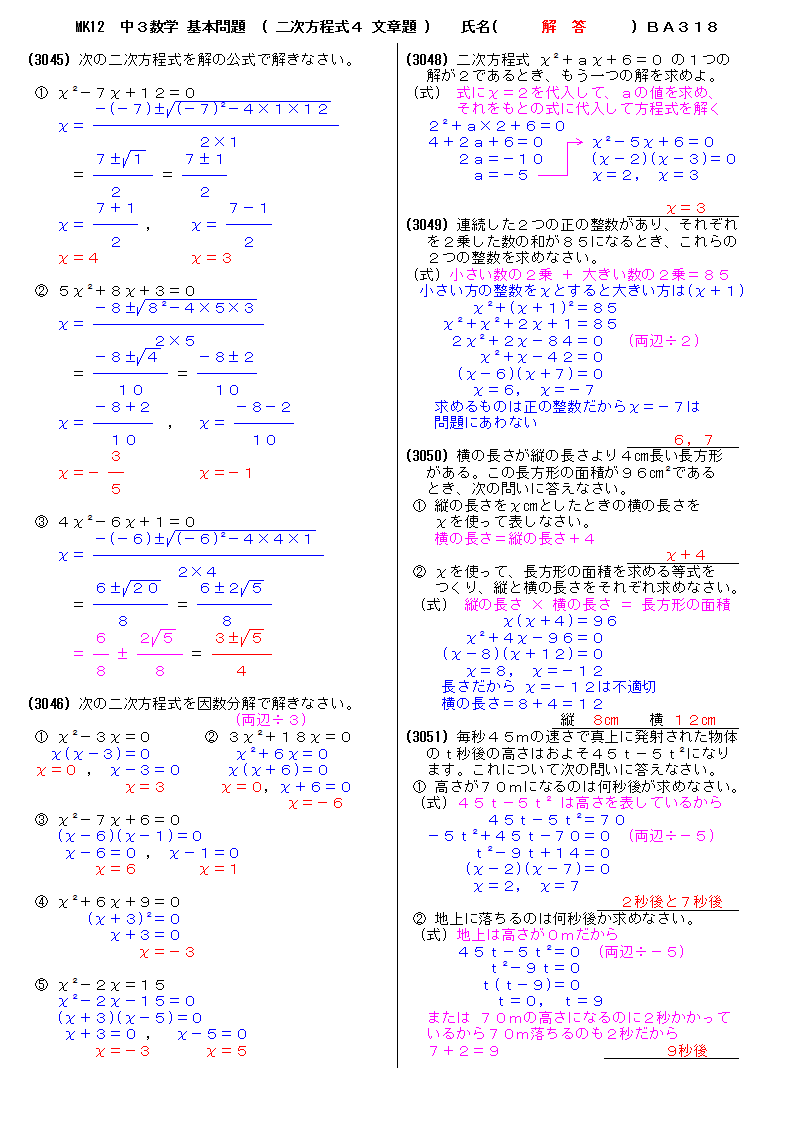



無料 中3数学 基本問題 解答プリント 318 2次方程式4 文章問題




中1 数学 中1 30 方程式を解く 小数と分数編 Youtube
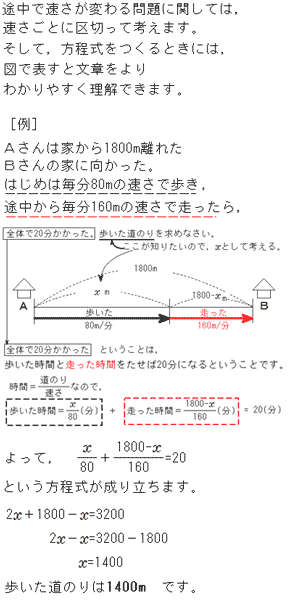



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座




中学1年生 数学 無料問題集 分数の一次方程式 おかわりドリル




方程式の解き方 簡単な問題で 解き方のコツを覚えよう 中学や高校の数学の計算問題



中1数学 基本 基礎問題 小数 分数の方程式の解き方 124
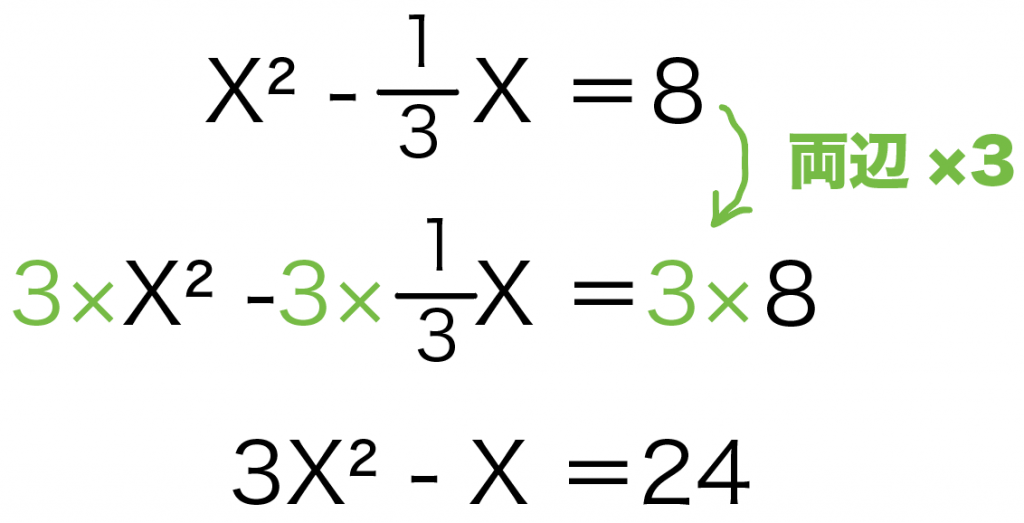



中3数学 分数を含む二次方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 方程式の解き方4 カッコ 分数 小数 例題編 映像授業のtry It トライイット



連立方程式の小数と分数の混ざった式について この問題が解 Yahoo 知恵袋




分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題




中学数学 一次方程式




分数と小数の連立方程式の解き方が分かりません 教えてください Clear




中2数学 黄色マーカーで塗った問題の 解き方をおしえてください Clear



1




連立方程式 加減法 計算ドリル 問題集 数学fun




因数定理を利用した因数分解の練習問題 高校数学の知識庫



不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典




中学数学 連立方程式 の効果的な教え方 小数 分数問題




分数形の不定方程式の解き方をイチから解説 数スタ




二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学



無料 中1数学 基本問題 解答プリント 方程式2 解き方1 123




中1 1次方程式 でつまずく原因と解決法 分数




電験3種書き込み式最強計算ドリル が出来上がるまで 電験3種 理論 最速合格




中1方程式 分数が含まれるときの解き方を問題解説 Youtube



Math 超速まとめ 方程式の解き方 働きアリ



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




数学 二次方程式 解の公式 分数の計算 hiroのアート トータルカウンセリング お悩み相談所rose



1




中学1年生 数学 無料問題集 小数の一次方程式 おかわりドリル



一次方程式の分数の問題の解き方 中学1年数学 一次方程式
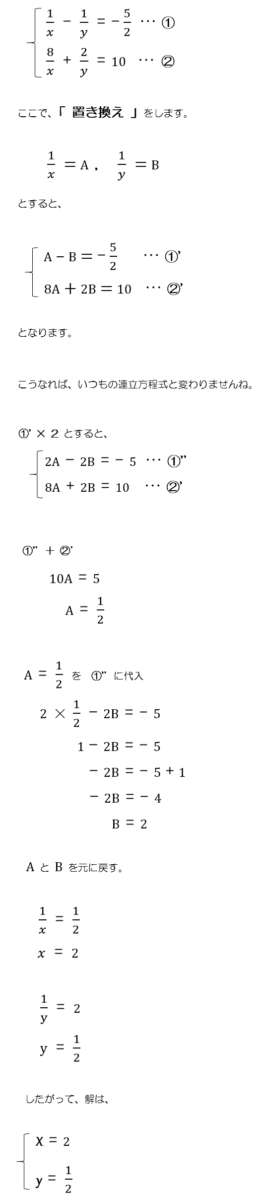



なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬




一次方程式の解の求め方 数学fun




中一数学 分数を使った方程式 の問題です 絶対間違ってるんで 解き 数学 教えて Goo




世界一わかりやすい数学問題集中1 3章 方程式




教えて下さい 連立方程式が分数の場合はどうやって解けばいいんですか Clear
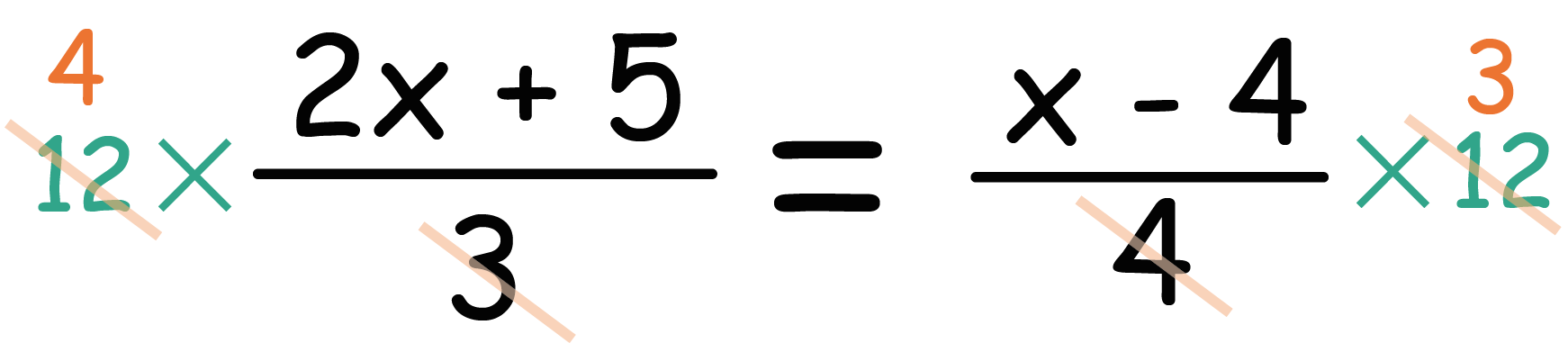



中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく




連立方程式 分数を含む計算の解き方をイチから解説 Youtube
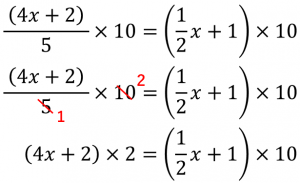



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題
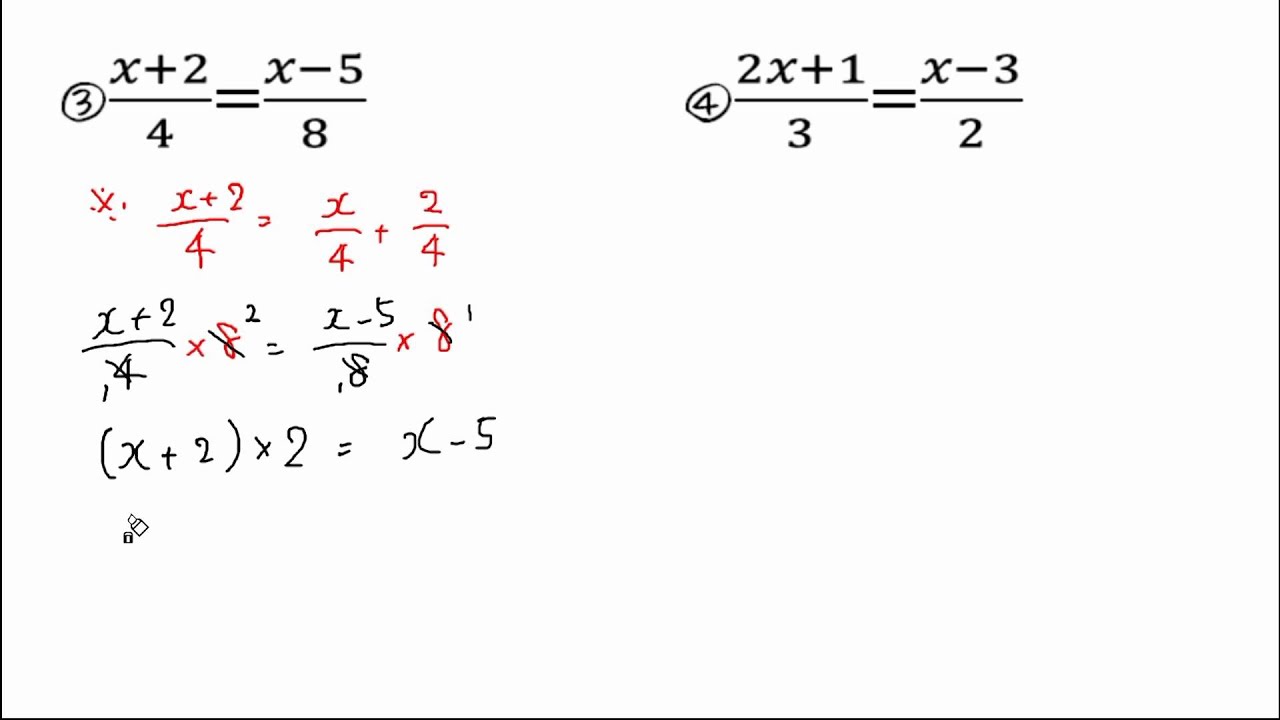



分数の入った方程式 問題 Youtube
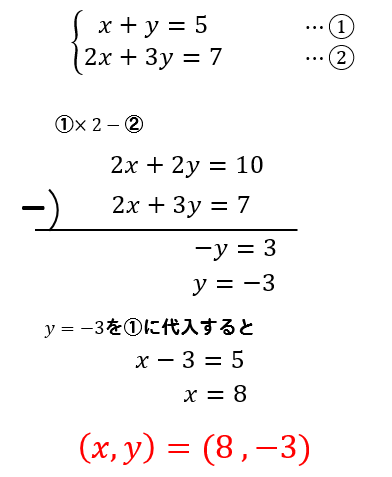



方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中学1年の数学 動画 方程式を解く 小数と分数編の問題 19ch




分数の入った方程式 Youtube




分数をふくむ連立方程式 Youtube




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点




中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
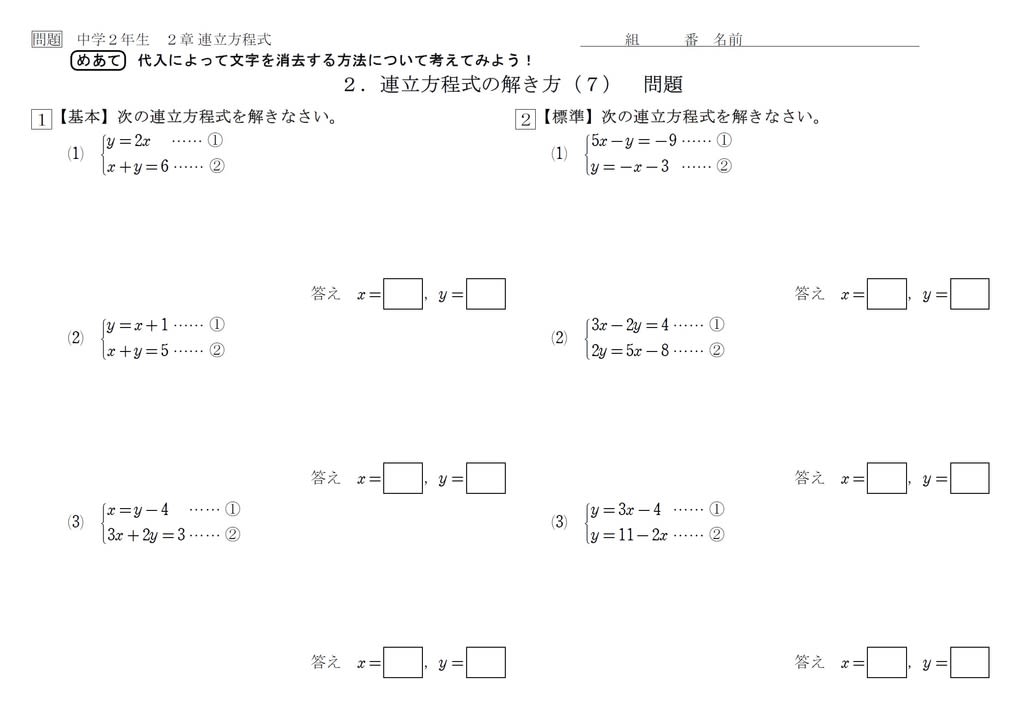



中2 連立方程式8 解き方7 中学数学の勉強に
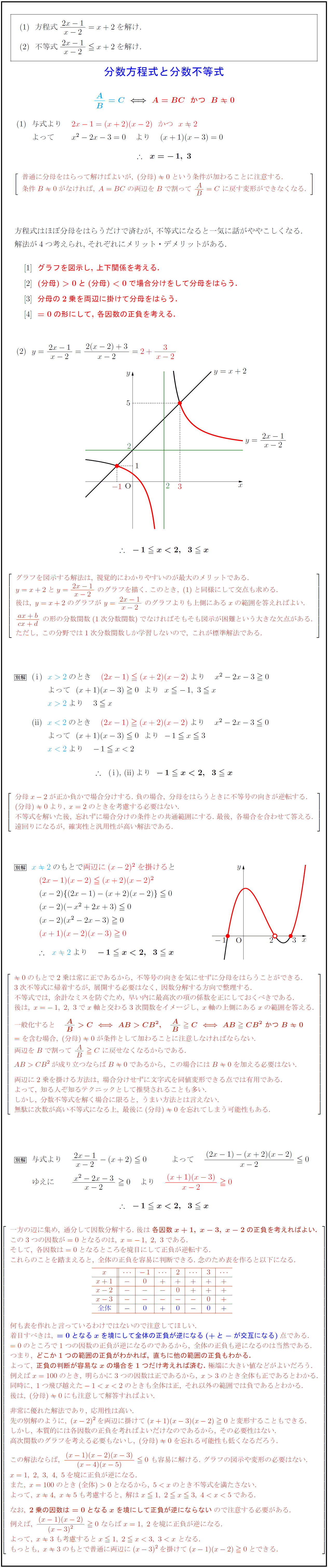



高校数学 1次分数方程式と1次分数不等式 受験の月
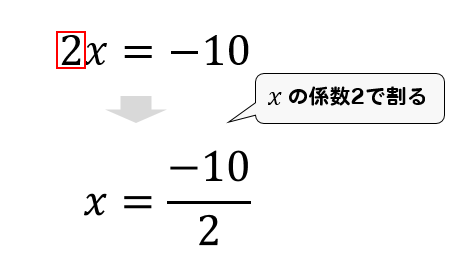



一次方程式の解き方を解説 かっこや分数の場合のやり方も 方程式の解き方まとめサイト




中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット
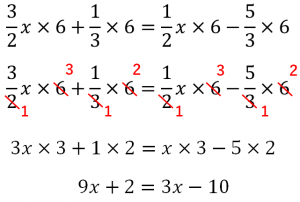



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu




一次方程式の解 計算ドリル 問題集 数学fun



中3数学 二次方程式の解き方と因数分解 解の公式の覚え方と簡単な計算問題 猫に数学



無料 中1数学 基本解説 解答プリント 方程式3 解き方2 124



中学の数学 分数の連立方程式の解き方について質問です の両辺に15 Yahoo 知恵袋




分数の方程式の解き方 分母を消せば中1の子でも絶対解ける 中学や高校の数学の計算問題



分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法



中2数学連立方程式文字が分母にある問題です 解き方を教えてく Yahoo 知恵袋
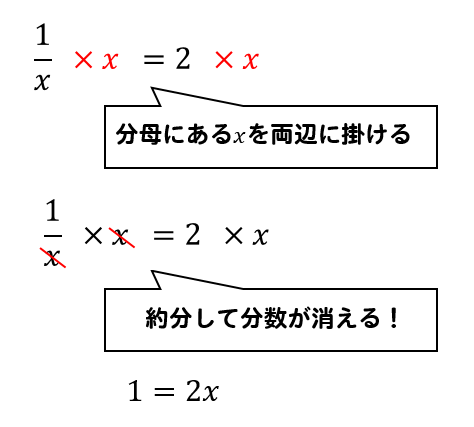



方程式 分母にxがあるときの解き方は 数スタ



1




中学3年数学 二次方程式 解の公式 確認問題2 あんのん塾
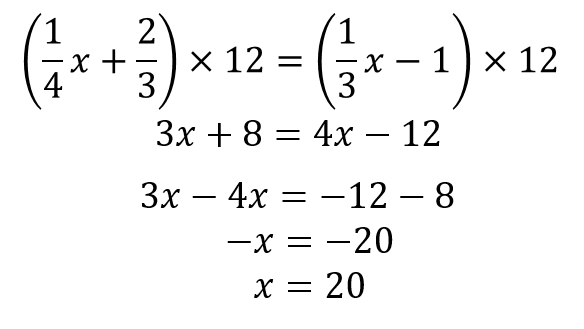



中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット



1




中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




連立方程式の解き方 係数に分数がふくまれる場合 Youtube




ねこ騙し数学




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者
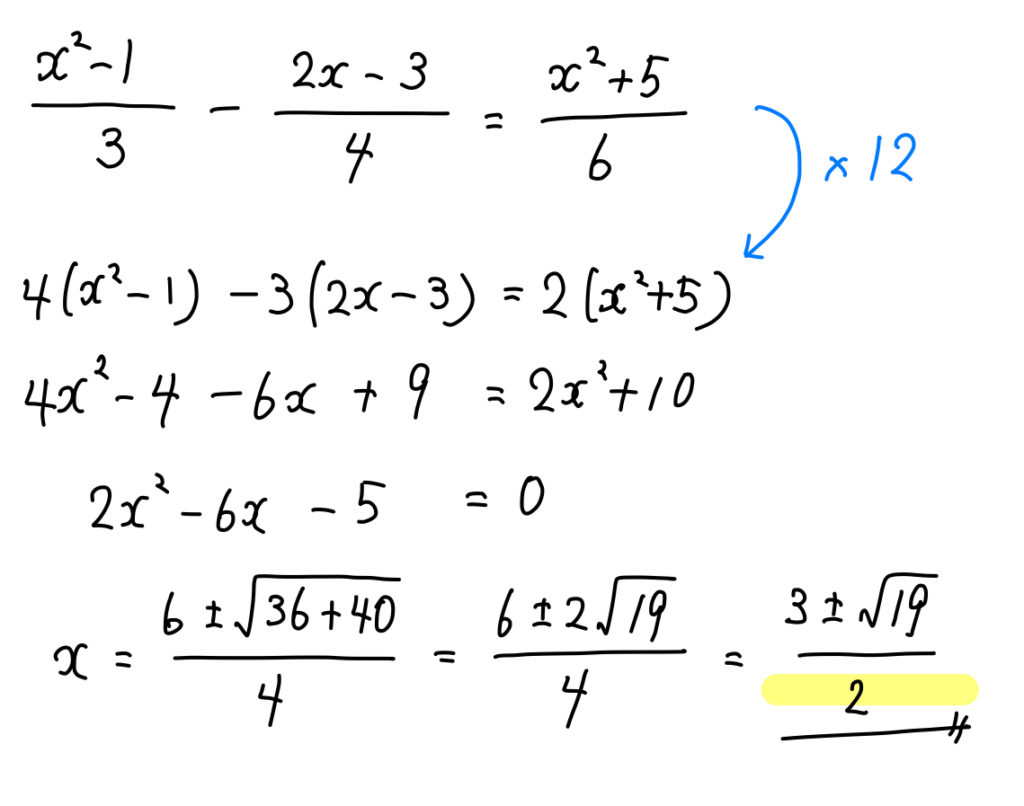



分数 小数 ルートを含む二次方程式の解き方まとめ 数スタ




方程式練習問題 連立方程式の文章問題 道のり 速さ 時間 方程式の解き方まとめサイト




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト
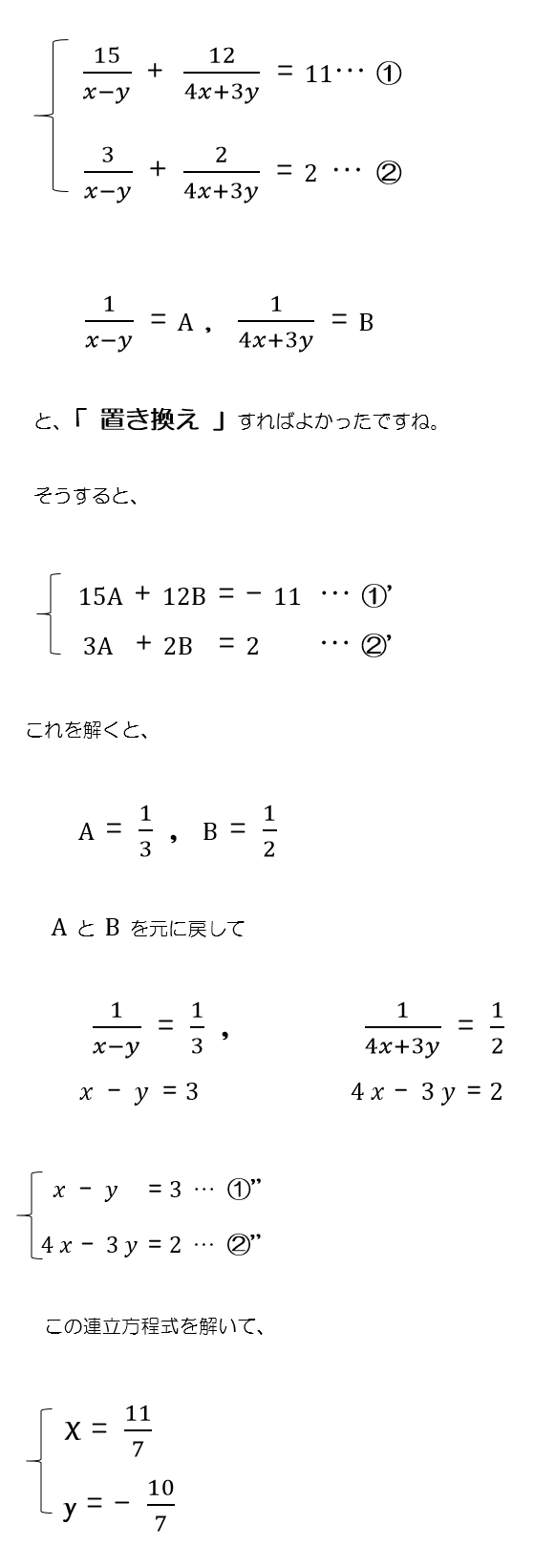



なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬




数学の高次方程式問題 解き方のコツ 公式 スタディサプリ大学受験講座



0 件のコメント:
コメントを投稿