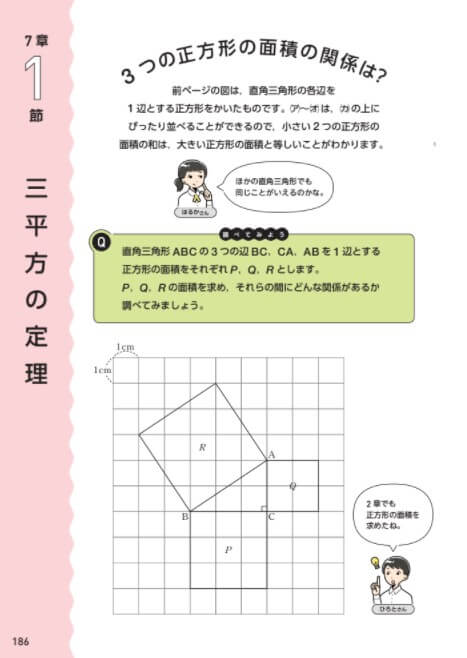
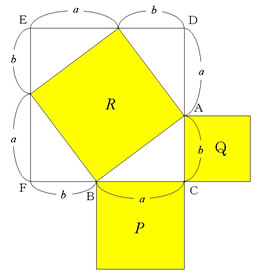
三平方定理1 2⑤ 2⑤ 右の図でAB=25、AD=15、BC=12のときACの長さを求めよ。 A B C D ABDは直角三角形で、2辺AB, ADの長さがわかるので、 三平方の定理でBDの長さが出せる。 BD2152 = 252 BD2 =400 よってBD= するとCD = BD BCから、CDの長さが出せる。 CD =12 =8 ACDは直角三角形で、AD=15, CD=8から 三平方の定理でACの長さが出せる。 152 = AC2 AC2 = 2About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators三平方の定理とは、直角三角形における各辺の長さに関する定理です。 証明したピタゴラスにちなんで、『ピタゴラスの定理』ともいわれます。 「斜辺(一番長い辺)の2乗」が、「他の辺の2乗の和」に等しいという定理です。 直角三角形の1辺の長さだけがわからない場合に、この定理を用いることで求めることができます。 また逆に、三角形の各辺について
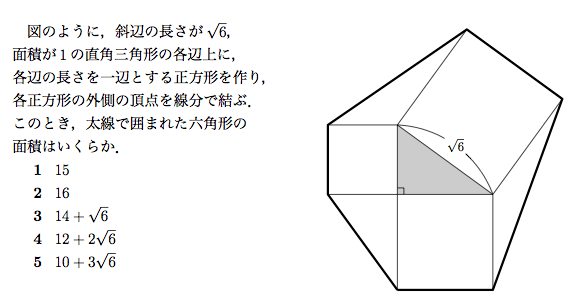
三平方の定理 二辺が等しく夾角が補角である三角形 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
三平方の定理 表面積
三平方の定理 表面積-このとき、三平方の定理を利用することによって、EB 2 の数字を計算することができます。 以下の通りです。 E B 2 = 7 2 5 2 = 74 それでは、辺BHの長さはいくらでしょうか。 BEHは直角三角形なので、三平方の定理を使うことができます。 またEB 2 の数字は分かっているため、以下のように辺BHの長さを計算できます。 B H 2 = 74 3 2 = B H = こうして、辺BHの長さは と計算 問題 問題三平方の定理・円錐の体積や表面積(中学3年生:第60回) 中学数学講座中3・三平方の定理動画講座一覧ページ 中学数学講座・動画一覧ページ テストの点・成績アップ・読解力・思考力の習得のカギは「自習力」! どんなに良い先生



3
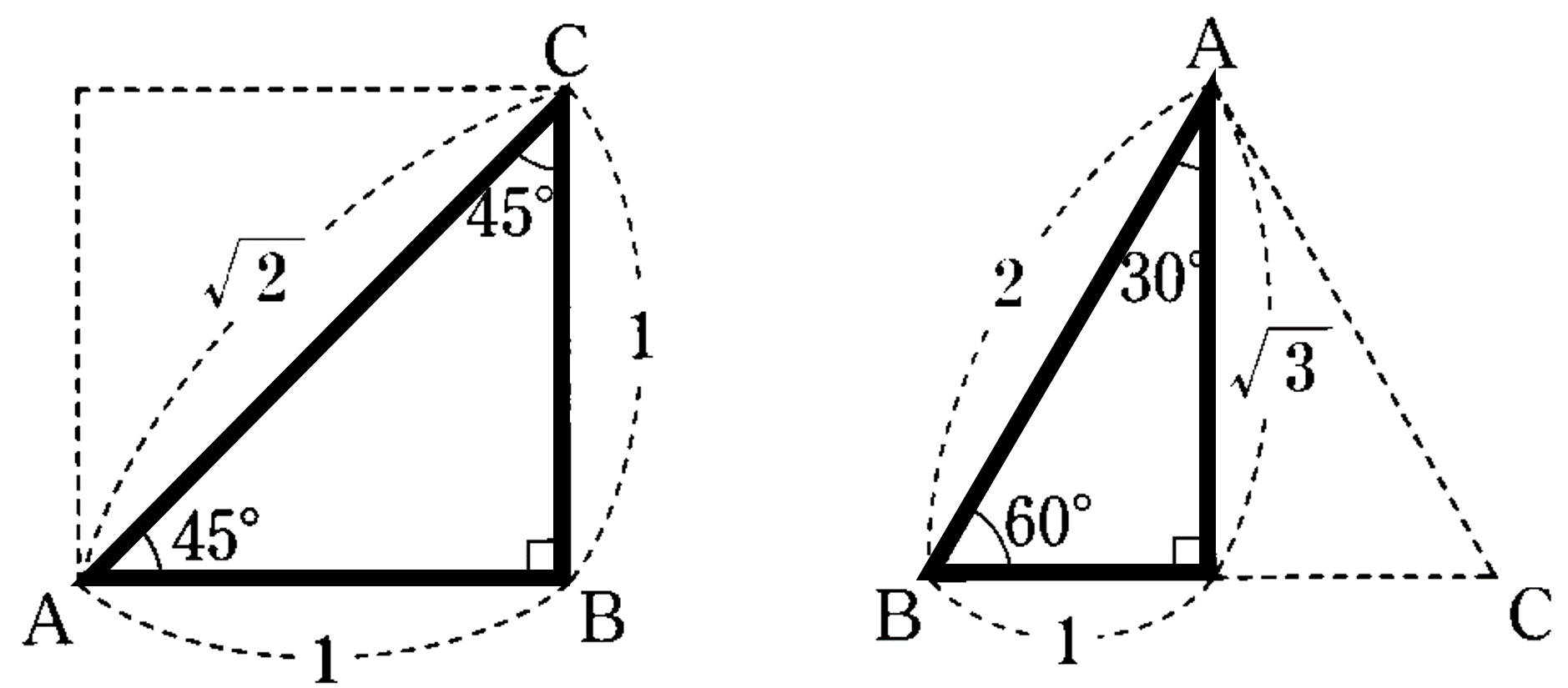
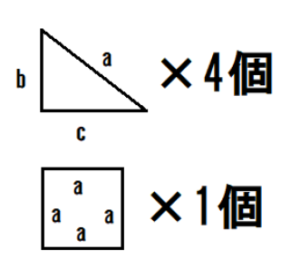
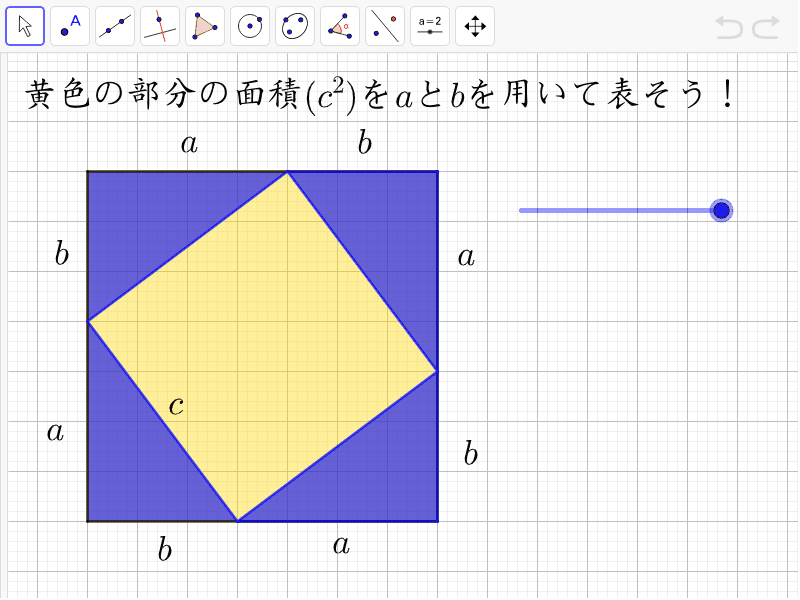
三平方の定理を使うと、直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます。 このページでは、三平方の定理を分かりやすく説明しています。中学校で学習する前の人にも、三平方の定理の意味を理解してもらえるような解説にしているので、ぜひお読みください。三平方の定理とは 三平方の定理は「ピタゴラスの定理」とも呼ばれ、直角三角形の3辺の長さの関係を表す式のことである。 図のように直角三角形の斜辺をc, 他の2辺をa, bとすると c2 = a2 b2の関係が成り立つ。 a b c a b c c 2 = a 2 b 2特別な直角三角形は 三角定規の $\textcolor{blue}{2}$ 種類 になります。 ① $\textcolor{blue}{30°,60°,90°}$ POINT:正三角形の半分 正三角形の $1$ 辺の長さを②とすると、$1$ 辺はその半分なので①となります。残り $1$ 辺を三平方の定理を使って求めると、
この記事の目次 三平方の定理の利用「最短距離の求め方」 (1)円すいの表面積の求め方 (2)おうぎ形の中心角の求め方3点セット (3)円すいの最短距離の求め方;Bm,cmがそれぞれの三角錐の高さとなる。(bm=cm= 3 2) a b c d m 底面 amdの面積を出す 表面積のときに出したとおりam = 3 3 2 同様にdm = 3 3 2 よって amdはam=dmの二等辺三角形である。 頂点mから辺adに垂線mnをおろすとnはadの中点なのでan= 3 2 三平方の定理よりam 2 = mn 2 an 2 なので (3 3 2) 2 = mn 2 (3 2) 2 27 4 = mn 2 9 4 mn 2 = 27 4 9 4 mn 2 = 18 4 mn = 3 2 2三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れて
三平方の定理応用(錐の表面積・体積) 次のそれぞれの立体の体積と表面積を求めよ。 底面の半径3cm, 母線の長さ5cmの円錐 5cm 3cm 体積 表面積 一辺6cmの正四面体 6cm 体積 表面積 底面が一辺10cmの正方形で、その他の辺がすべて13cmの正四角錐 13cm 10cm 体積 表面積 三平方の定理とは、いわゆるピタゴラスの定理と言われるもので、直角三角形の辺に関する公式です。 まずは以下の図をみてください。 斜辺(c)を二乗したものは、他の辺 (aとb)をそれぞれ二乗したものの和に等しくなる、というのが三平方の定理の公式三平方の定理の解説 直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。 ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。



名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 ひ ではじまるキーワード キーワード ピタゴラスの定理 公式と図形




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
(三平方の定理) 折り紙を重ねて(三平方の定理) 正四面体の体積(立方体を利用して) (三平方の定理) 正三角形の内部にひそむ定数(三平方の定理) 正四面体の高さを求めよう(三平方の定理) コップの中に入る水の量は?(三平方の定理) 三平方の定理 基礎数学 基礎数学 ピタゴラス ピタゴラスの定理 三平方の定理、三平方 計算 設計・計算ポータルサイト 設計・計算ポータルサイト 本のサイズ 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



7章 三平方の定理 タカラゼミ
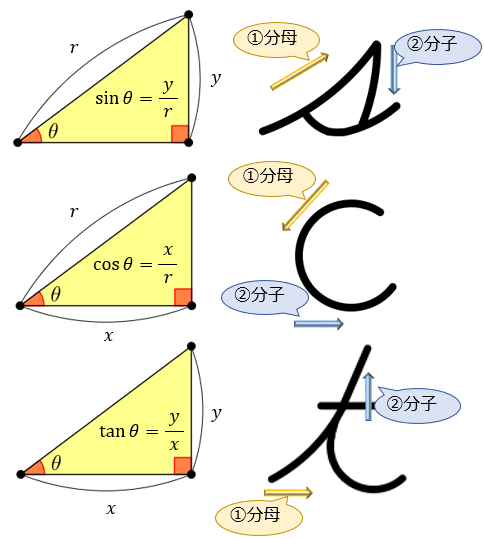
三平方の定理は、直角三角形の辺の長さの関係を表す定理です。 直角三角形の斜辺の長さをa,残りの2辺の長さをb,cとすると、 a^2=b^2+c^2 という関係が成り立ちます。 a,b,cの文字のどれがどこにいくかよりも、「斜辺がどれか」が大切です。 「斜辺の2桃 《三平方の定理》 《解説》 次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.) これを用いて3辺の長さのうち2辺の長さが分かっているとき,残りの1辺の長さを求めることができます 三平方の定理 法長 X=√Y²Z² 高さ Y=√X²Z² 底辺 Z=√X²Z² 三角関数 sinθ=Y/X(高さ÷法長) cosθ=Z/X(底辺÷法長) tanθ=Y/Z(高さ÷底辺) 勾配 (高さ底辺) 角度 3分 (103) 73°18'03" 5分 (105) 63°26'06" 8分 (108) 51°'25" 1割
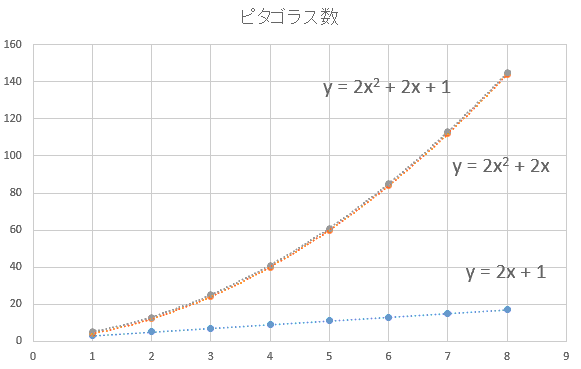



数の不思議 奇数の和でできるピタゴラス数 Note Board




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
三平方の定理(ピタゴラスの定理)の公式 にぶち込めばいいんだ。 x² = 5² 12² x = 13 直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。 なっ。 向きが変わると、斜辺がどれなのかうっかりしてしまうよ。 要注意だな。 Step2 「平方根の計算混じってるタイプ」 2つ目のタイプは、 三平方の定理の計算に「 平方根・ルートの計算 」が混じってるやつだ。 たとえば、次の 三平方の定理は、直角三角形の斜辺の2乗が他の辺の2乗の和に等しい、という公式です。 非常に便利ですが、二次方程式になってしまうので解答するのに時間がかかります。 そこで、テストによく出てくる直角三角形については暗記してしまいましょう。 ここでは、特に重要な7つのパターンをご紹介します。 こちらは非常に有名な直角三角形です。 3つのざっくりと分けてもこれだけの知識がある。 これらの中で特に大切な知識は 相似 と 三平方の定理 である。 なぜなら作図はできるに越したことはないが、実 生活でも入試でもあまり使わない 。




三平方の定理の利用 Ict教材eboard イーボード




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi
三平方の定理の歴史は、 紀元前1800年頃のバビロニア (今のイラク南部)にさかのぼります。 バビロニアでは、今で言う ピタゴラス数( a 2 b 2 = c 2 ~a^2b^2=c^2~ a 2 b 2 = c 2 を満たす自然数の組 ( a , b , c ) ~ (~a~,~b~,~c~)~ ( a , b , c ) )に関する数表 が存在していました。 あわせて読みたい 数学史3-7 ~バビロニアの三平方の定理~ 三平方の定理の最初の発見者 三平方の定理でのとき√6√2√6√24という直角三角形の比がありますが、なぜこのような比になるのか教えて下さい。 abc ∠a=75°∠b=15° ∠c=90° という abcを使って説明してください。 中学校で習う範囲までで分かるようにお願いします。三平方の定理 は,2辺の長さをa,b,斜辺の長さをcとする直角三角形において成り立つ,次の定理です。 斜辺cの2乗は,他の辺a,bをそれぞれ2乗した数の和に等しいのですね。 直角三角形では,2つの辺の長さがわかると,三平方の定理を使って他の1辺の長さが計算できる ことを覚えておきましょう。 また, 三平方の定理の逆 も成り立ちます。 3辺の長さがa,b,c




三平方の定理 覚えておきたい基本公式を解説 数スタ
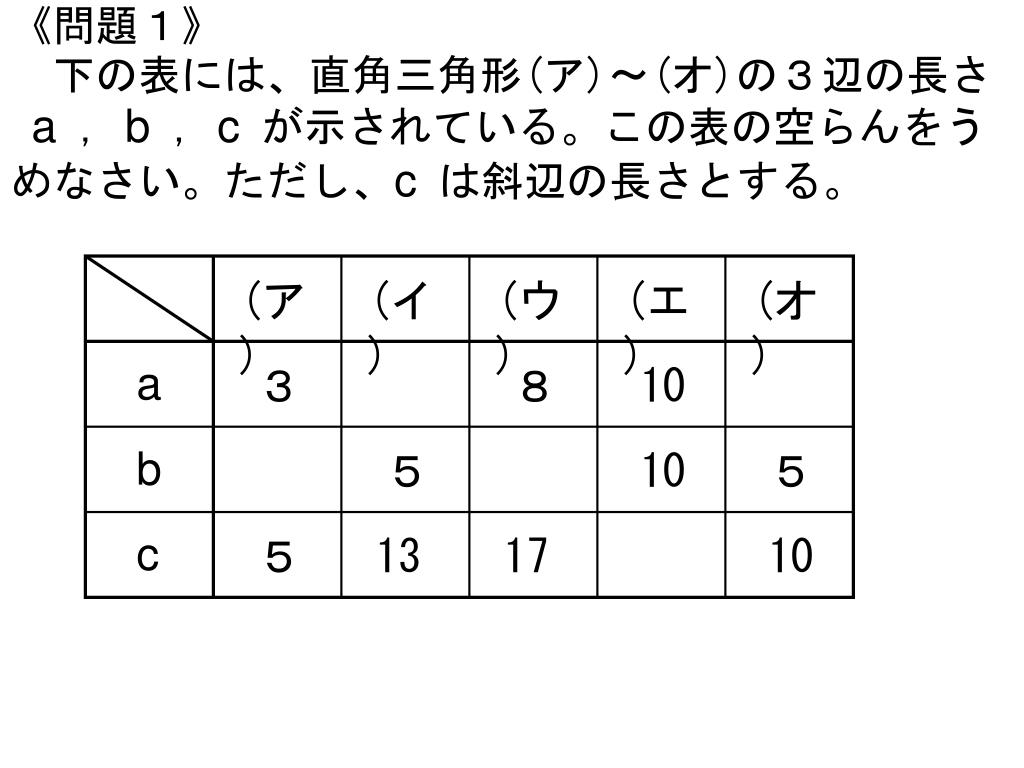



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id
三平方の定理の活用三平方の定理を活用して,以下のようなものを求めることができる。 正方形の対角線の長さや,三角形の高さ 弦や接線の長さ 座標が与えられた2点間の距離 直方体の対角線の長さや,角錐,円錐の高さ特別な直角三角形の3辺の長さの比直古代のインドにおいては三平方の定理を満たすようないくつかのピタ ゴラス数の組み合わせが見つかっていました。しかし、数学的に正しいと わかっていたわけではなく、経験的に具体的な数の組み合わせを知ってい たのであろうと考えられています。 5 たとえば、「5:12:13」をそれぞれ2倍した「10:24:26」も三平方の定理を満たします。 ①辺の比が3:4:5 ピタゴラス数の中で、もっともシンプルで有名な組み合わせが3:4:5です。 三平方の定理で確かめてみましょう。 3²+4²=9+16=25=5²
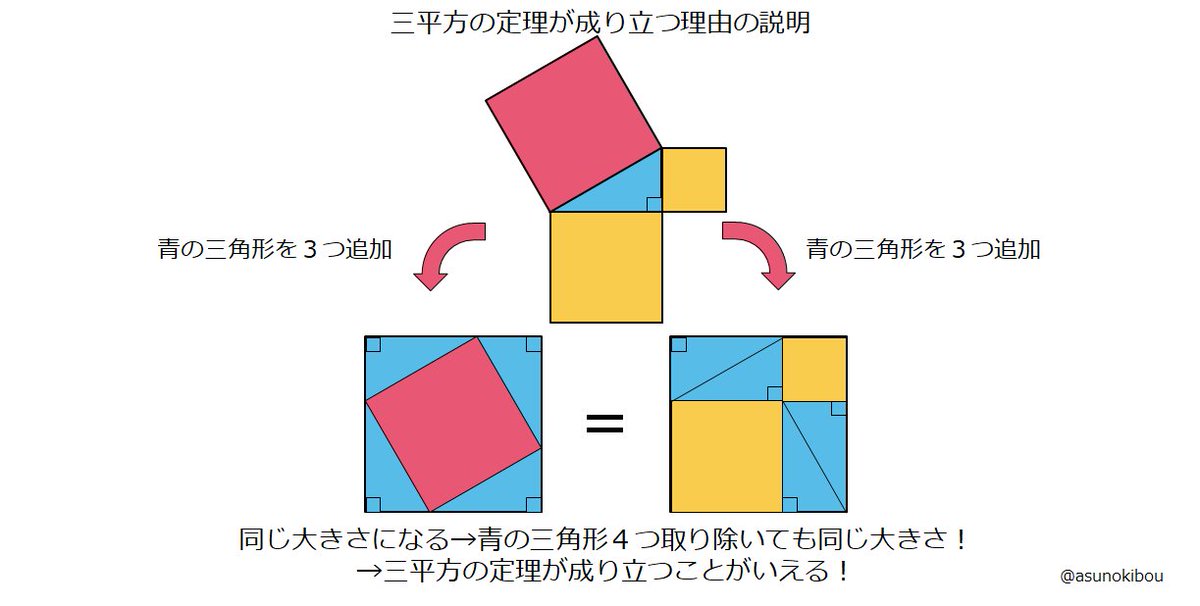



三平方の定理 ピタゴラスの定理 を分かりやすく表した動画 Togetter




中学3年の数学 動画 三平方の定理 基本編の問題 19ch




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club
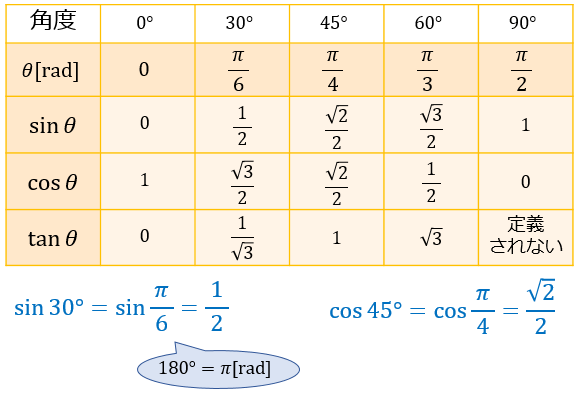



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ



数学のコツ 三平方の定理 個別指導ソラオトのスタッフブログ



3



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室
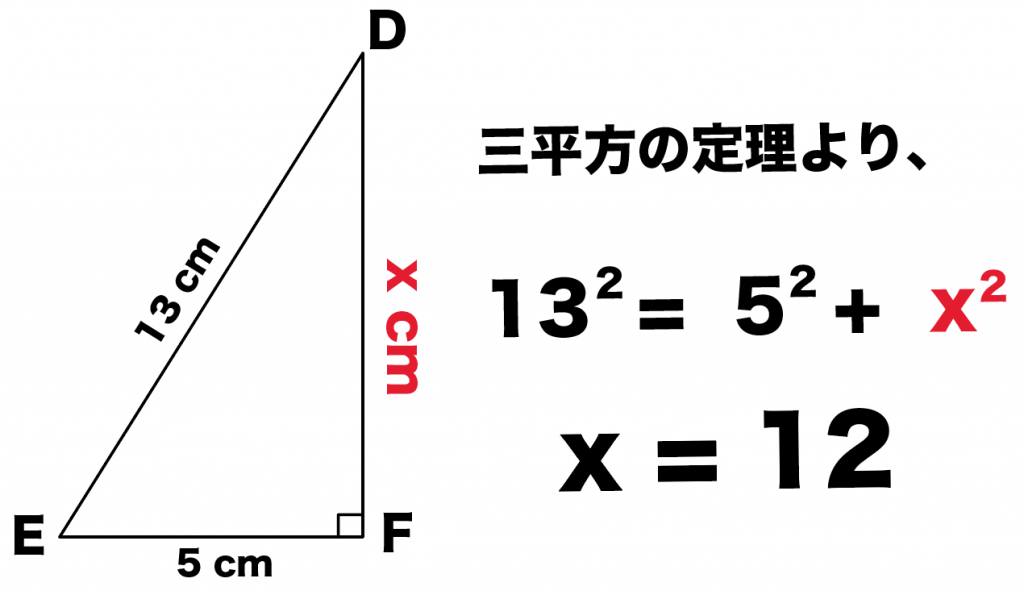



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



3




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三角比 高校物理の備忘録




無料 中3数学 基本解説 問題プリント 336 三平方の定理4 空間図形



三平方の定理から円周率を計算してみる Yamav1 02bのブログ



三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba



三平方の定理
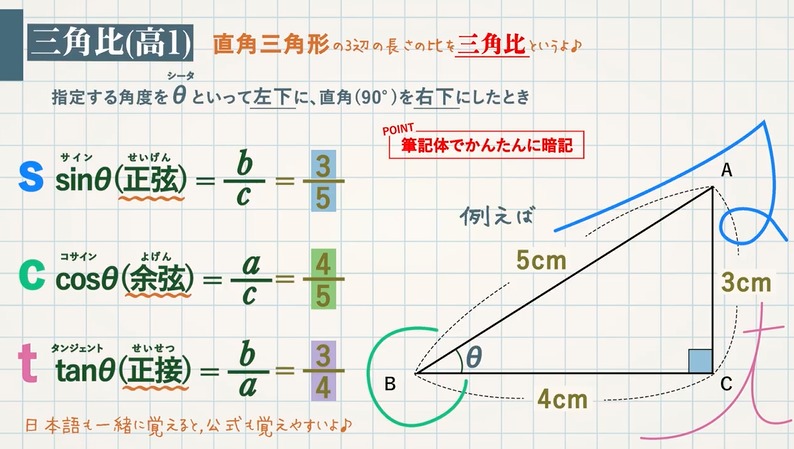



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



2



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




三角比を用いた計算問題をマスターしよう スタディクラブ情報局




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学



三平方の定理



三平方の定理の証明 ピタゴラス Geogebra



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ




中学3年の数学 動画 三平方の定理 練習編の問題 19ch



1




三平方の定理 二辺が等しく夾角が補角である三角形 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




15 シリーズの三角比 おいしい数学



三平方の定理 練習問題 苦手な数学を簡単に




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理から四立方の定理へ 東京図書出版
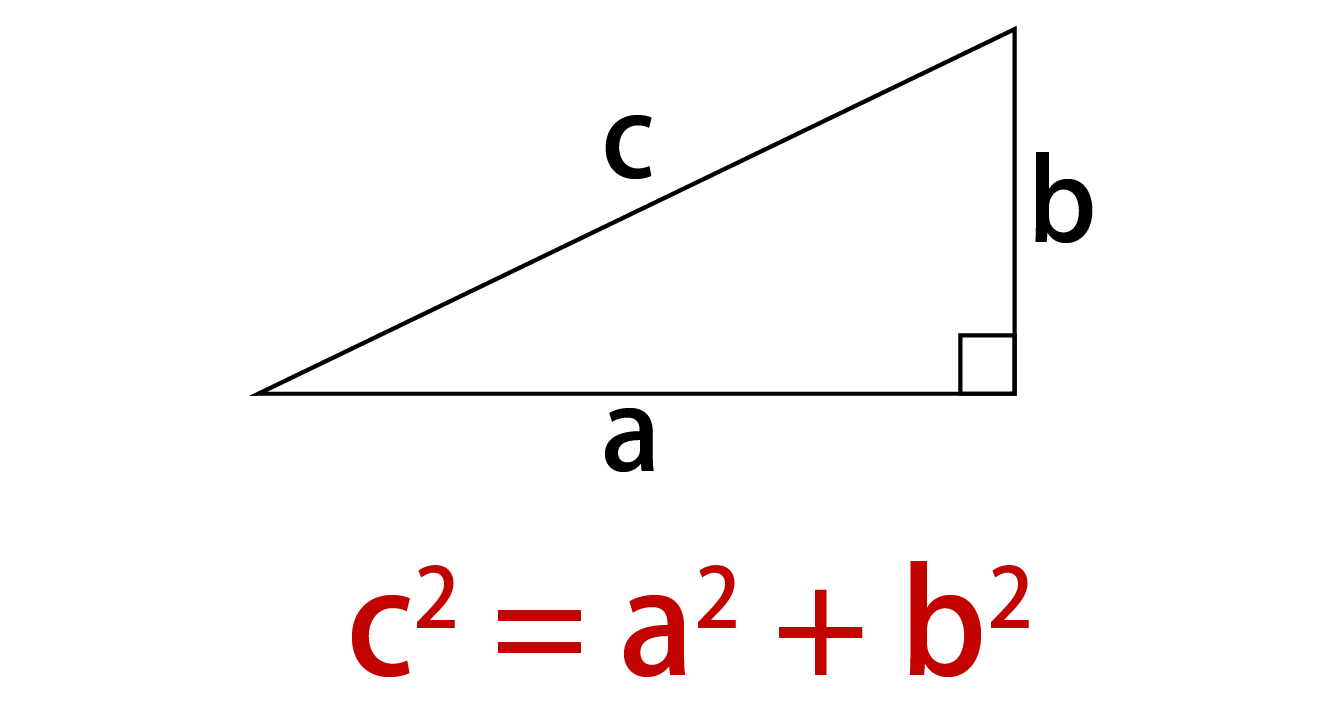



三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




わかりやすい三角比と基本公式 Irohabook




Plotly で 表 を描く方法 2 Figure Factories Aiリサーチコレクション




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 を分かりやすく表した動画 Togetter




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




神奈川県公立高校入試 出題範囲 あすもりのブログ



3年7章 三平方の定理 Math Connect 東京書籍 先生のための算数数学ポータルサイト




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi
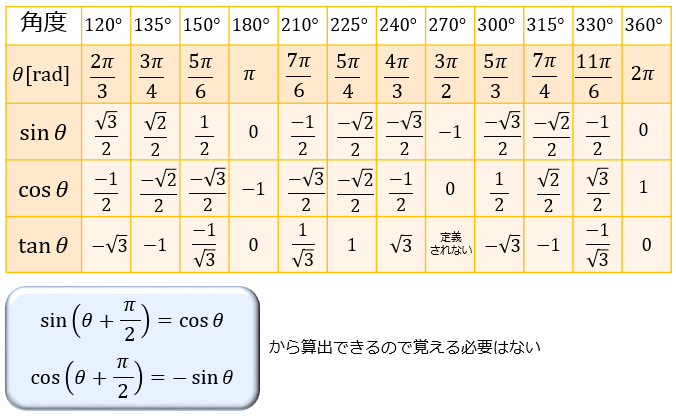



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ



三平方の定理 やややさしい数学



三平方の定理




三平方の定理 相似を利用した問題 問11の 2 を教えてください Clearnote



1
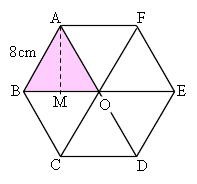



Mathematics 三平方の定理 3 いろいろな三角形 働きアリ




三平方の定理 自動計算サイト
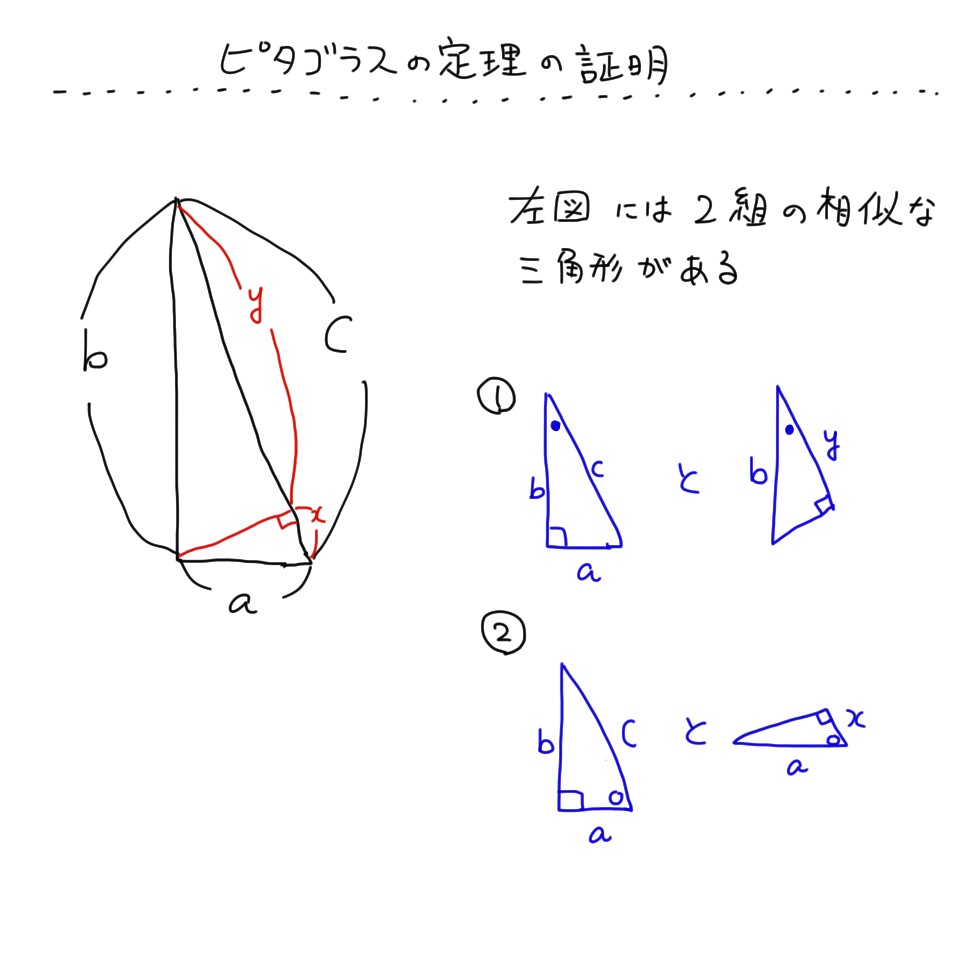



中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
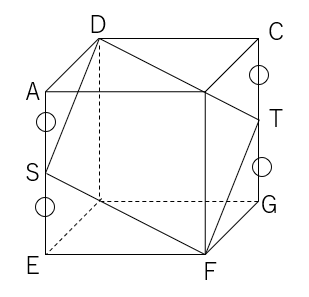



三平方の定理と影の面積 数学の要点まとめ 練習問題一覧
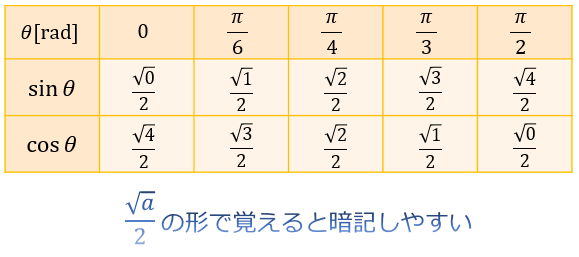



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club



三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba




特別な直角三角形の3辺の比 三平方の定理 中学生からの勉強質問 数学 進研ゼミ中学講座




都立入試数学 三平方の定理を使わなくても解けるか 都立に入る
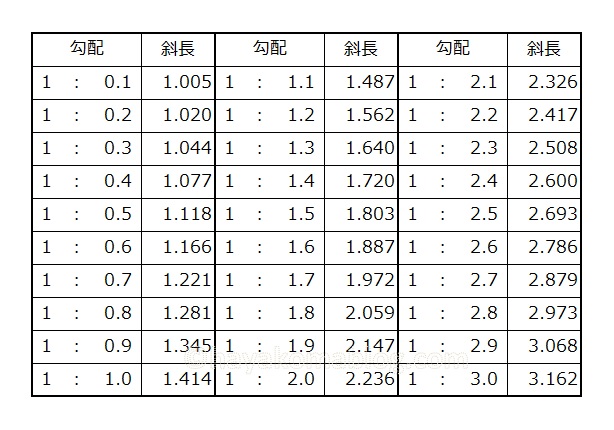



勾配 斜長 法長 斜辺 換算表
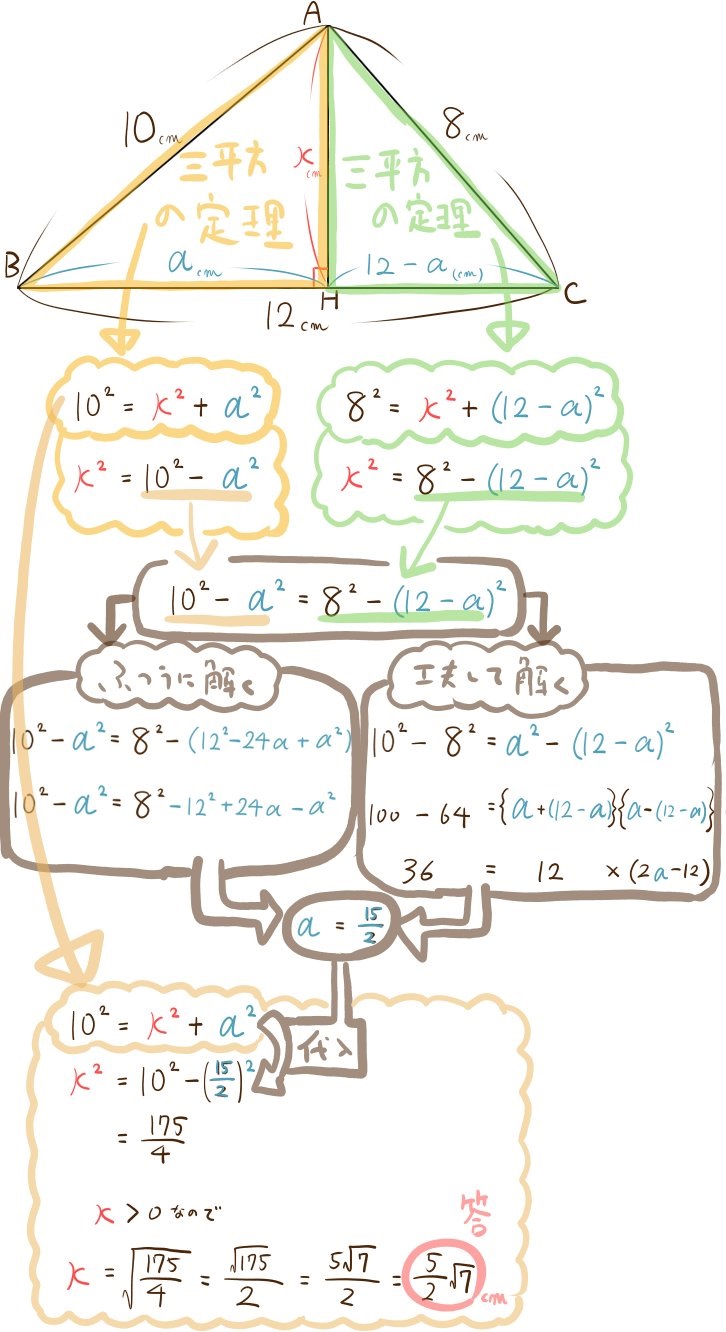



三平方の定理を使う平面図形の難問たち 中学数学 高校入試 坂田先生のブログ




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
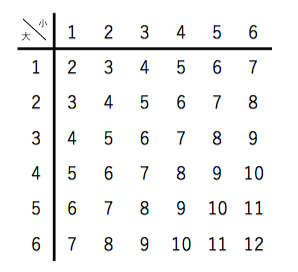



確率の基本 サイコロを投げる 苦手な数学を簡単に



3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist
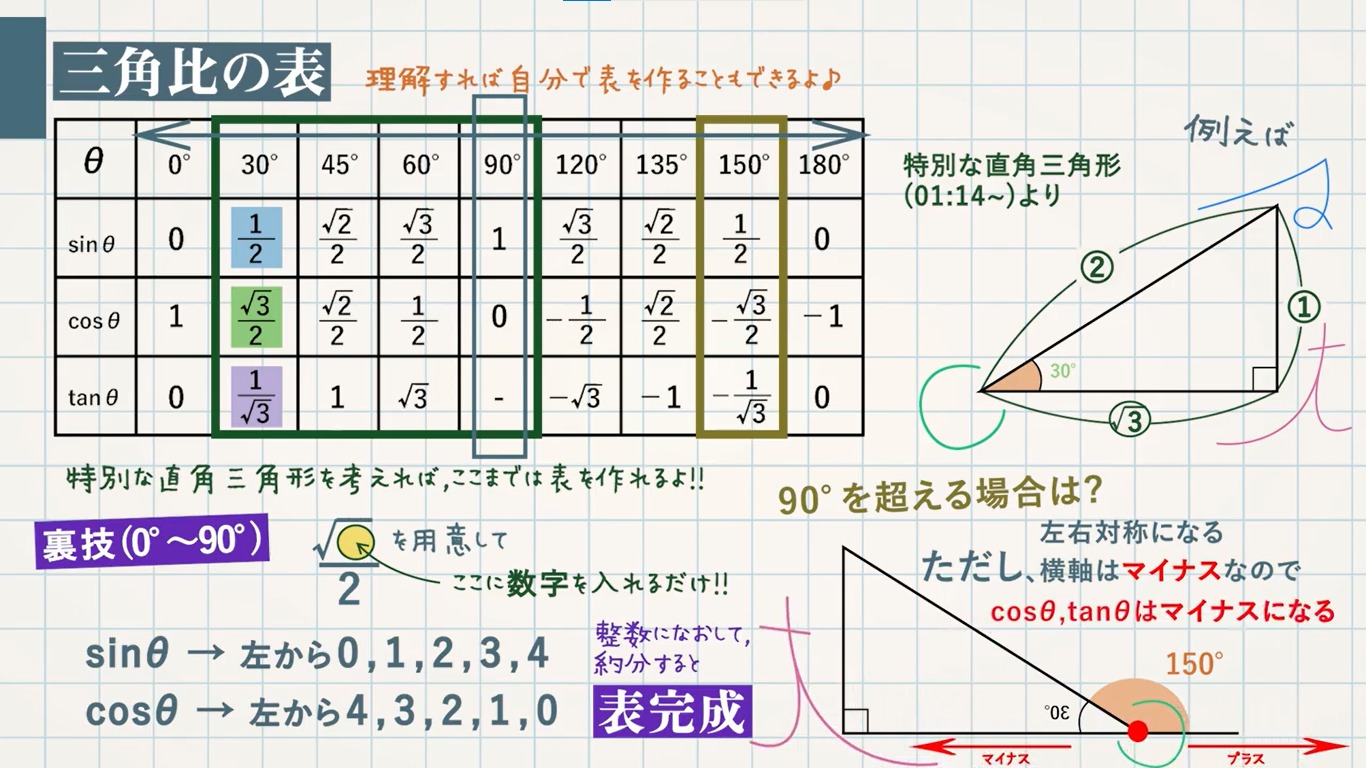



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理の練習問題が分からないので教えて欲しいです Clearnote
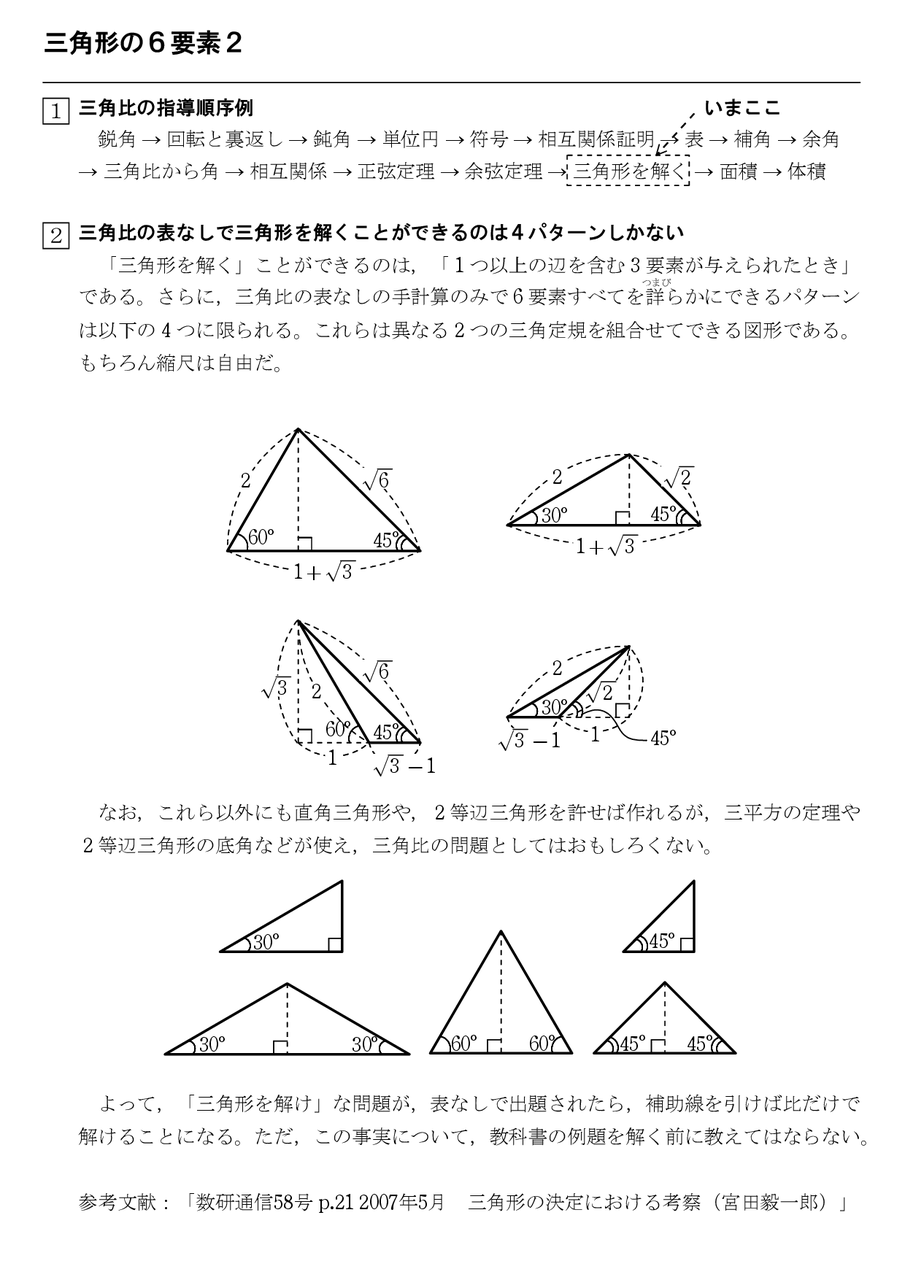



三角形の6要素2 怜悧玲瓏 高校数学を天空から俯瞰する
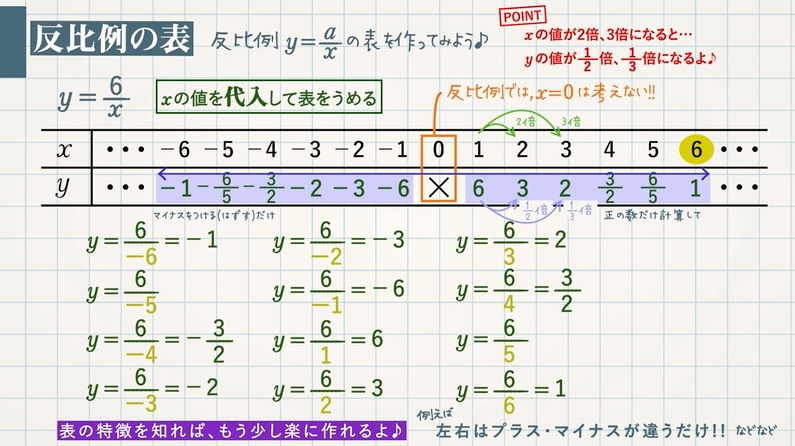



反比例の表とグラフ 教遊者
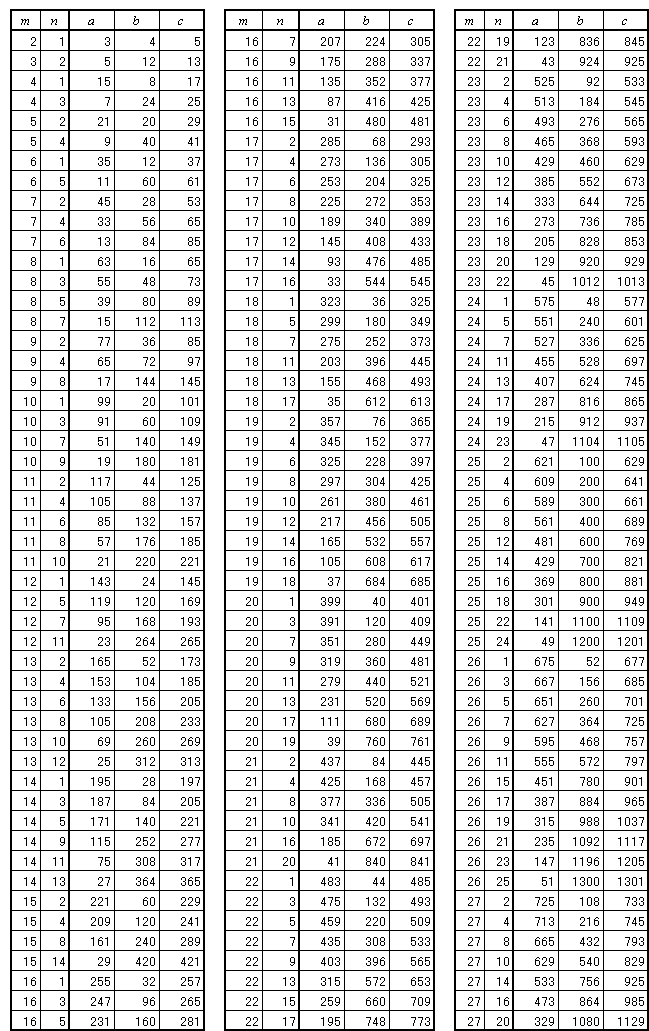



書評 ピタゴラスの定理




三平方の定理 覚えておきたい基本公式を解説 数スタ



三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
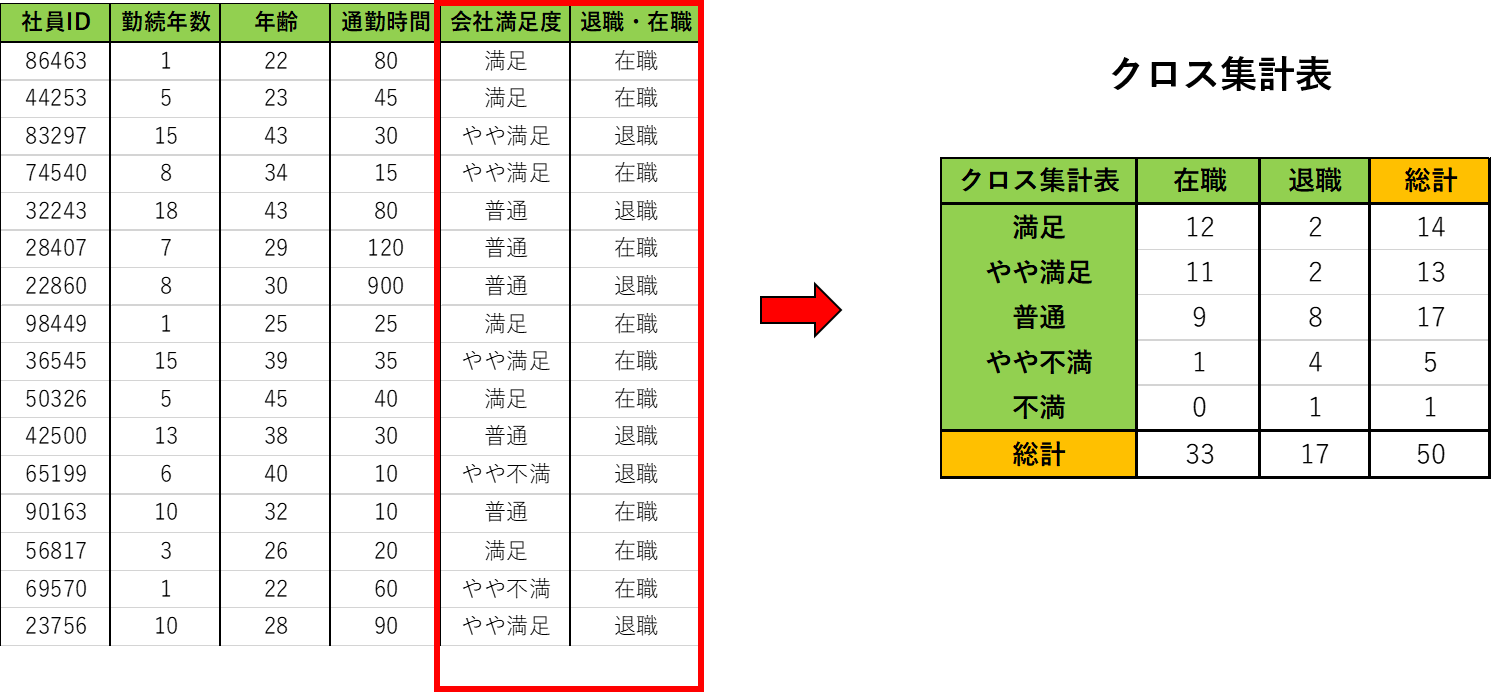



はじめての統計学 データの関係性を見る クロス集計表 数学 統計教室の和から株式会社



三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba
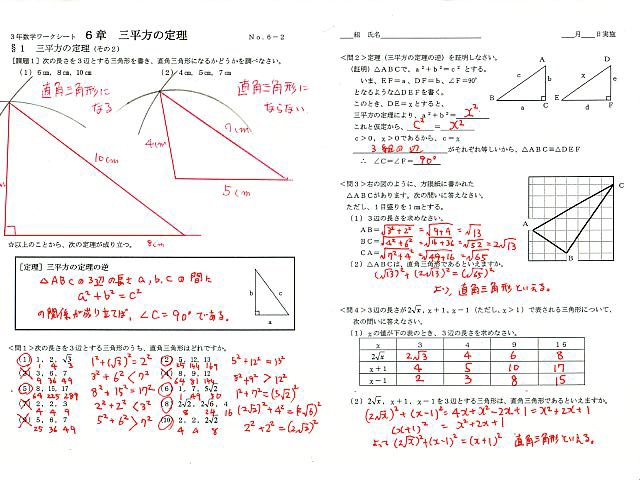



2 三平方の定理の逆 Mathweather4067のblog




三平方の定理 高校入試 数学 良問 難問
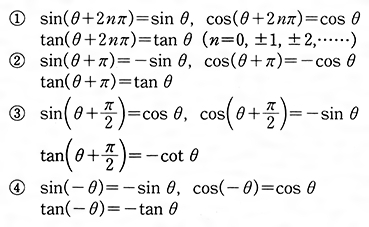



三角関数とは コトバンク
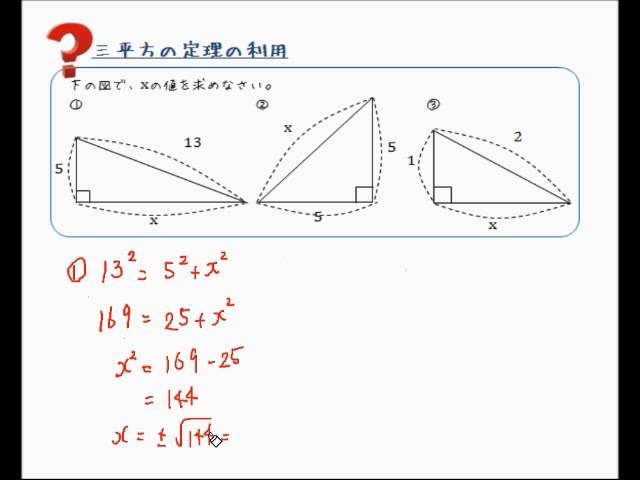



三平方の定理で辺を求める Youtube




三平方の定理 セルモ大蔵 世田谷 の塾長ブログ




三平方の定理 膨大なページ数 Wiki




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




3 4 5の三角形で 本当に直角ができる Note Board




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
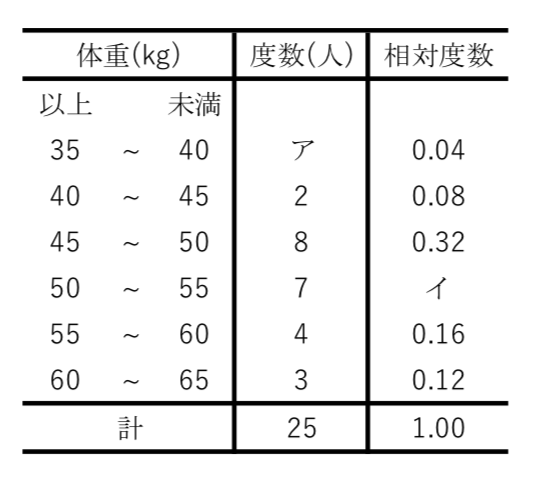



度数分布表を完成させよう 求め方は決まっている 苦手な数学を簡単に




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




わかりやすい三角比と基本公式 Irohabook




三平方の定理 セルモ大蔵 世田谷 の塾長ブログ




コラム ピタゴラスの定理 江戸の数学



Ten Tokyo Shoseki Co Jp
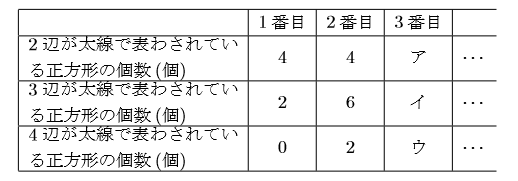



中学数学 中1規則性 数樂管理人のブログ




ピタゴラスの定理 三平方の定理 ベクター イメージマート



三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理 中3数学 3学期期末テスト用 教科書178 1 赤城 ᐡᐤᐡ



0 件のコメント:
コメントを投稿